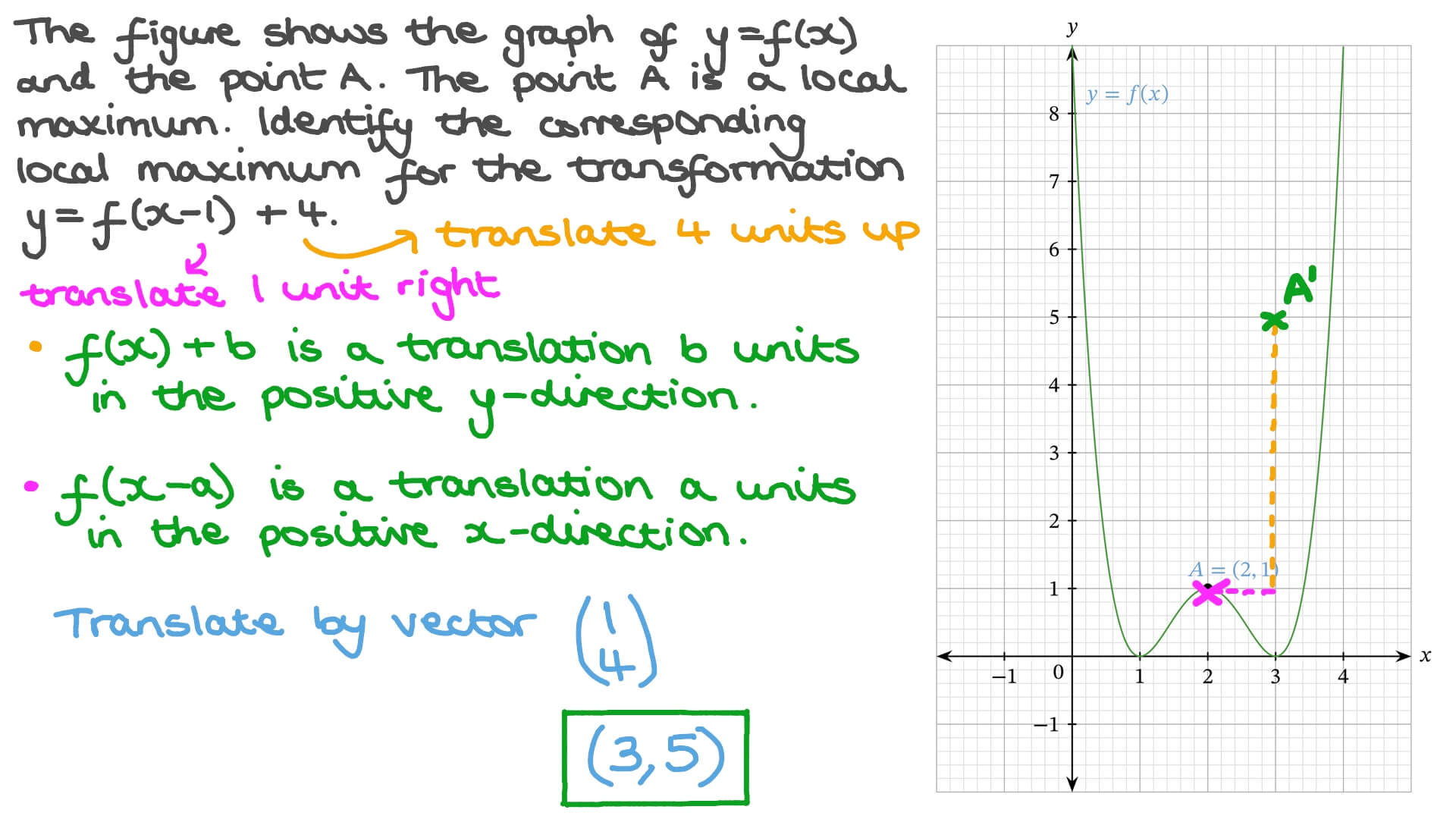
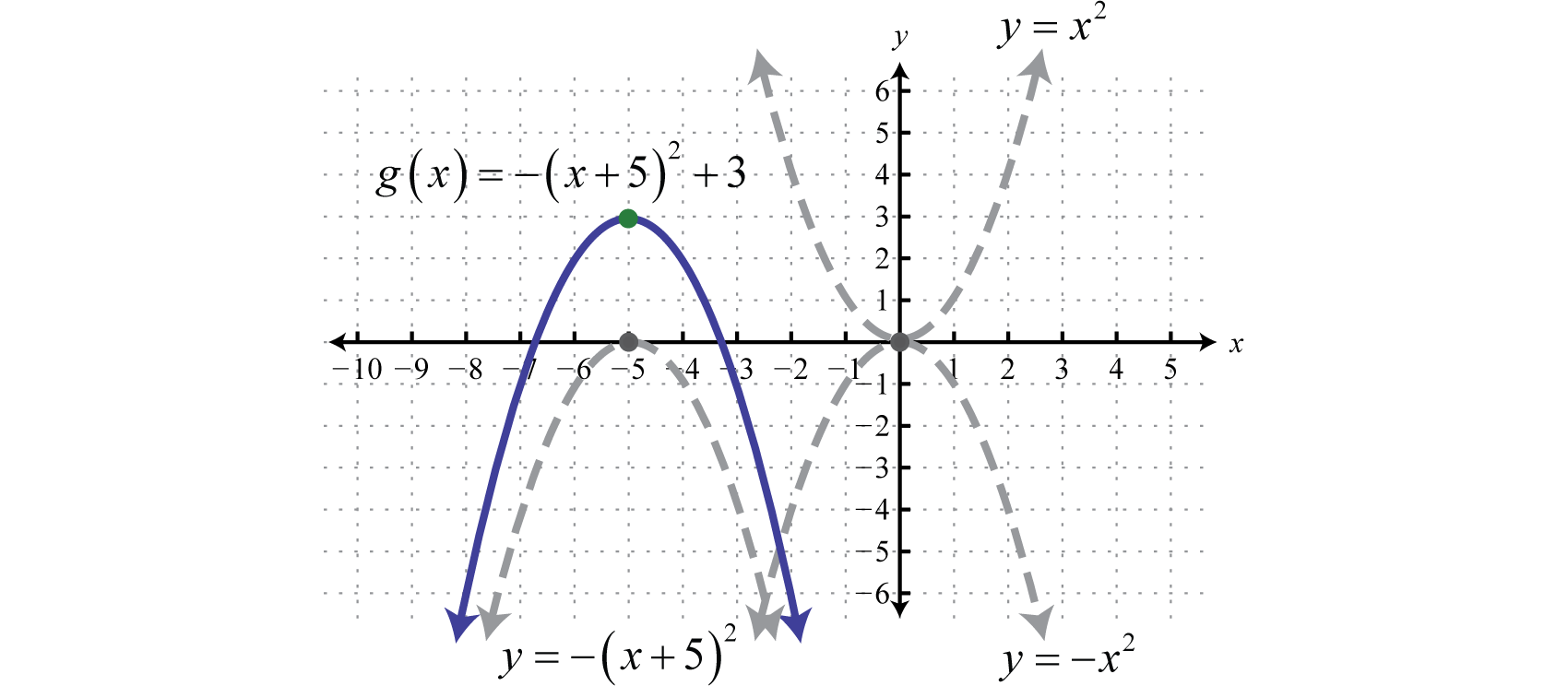
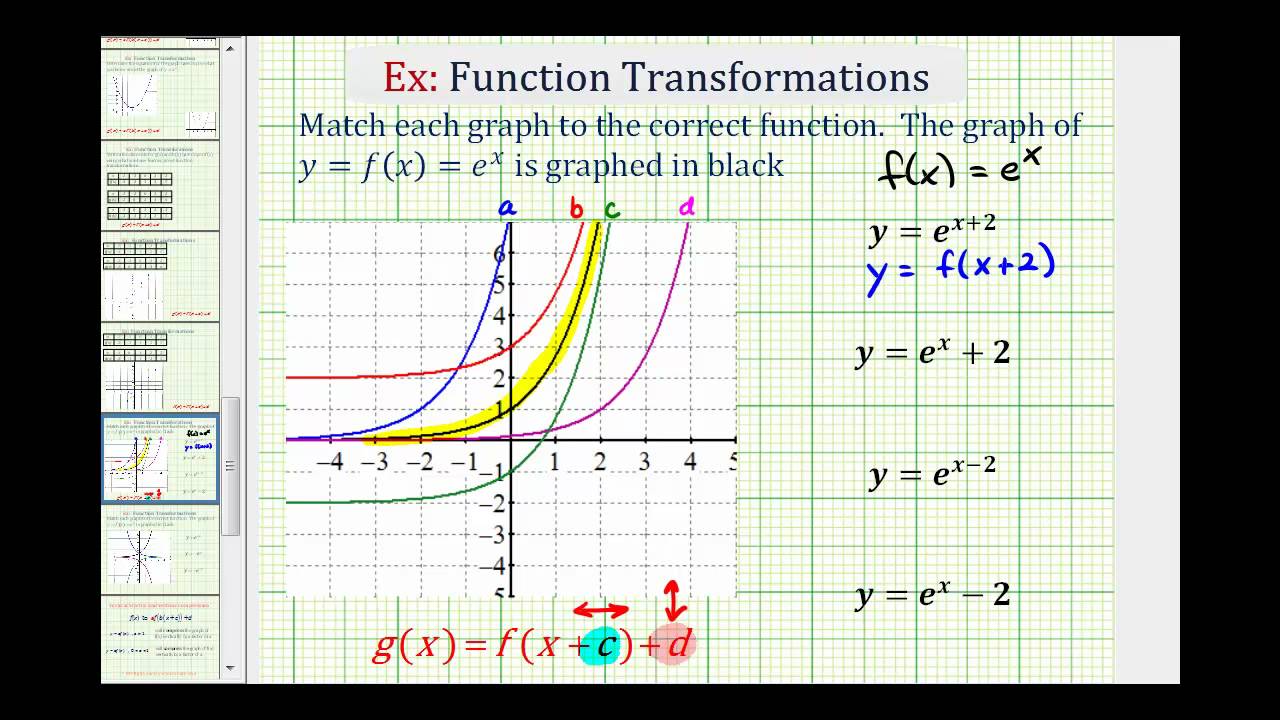
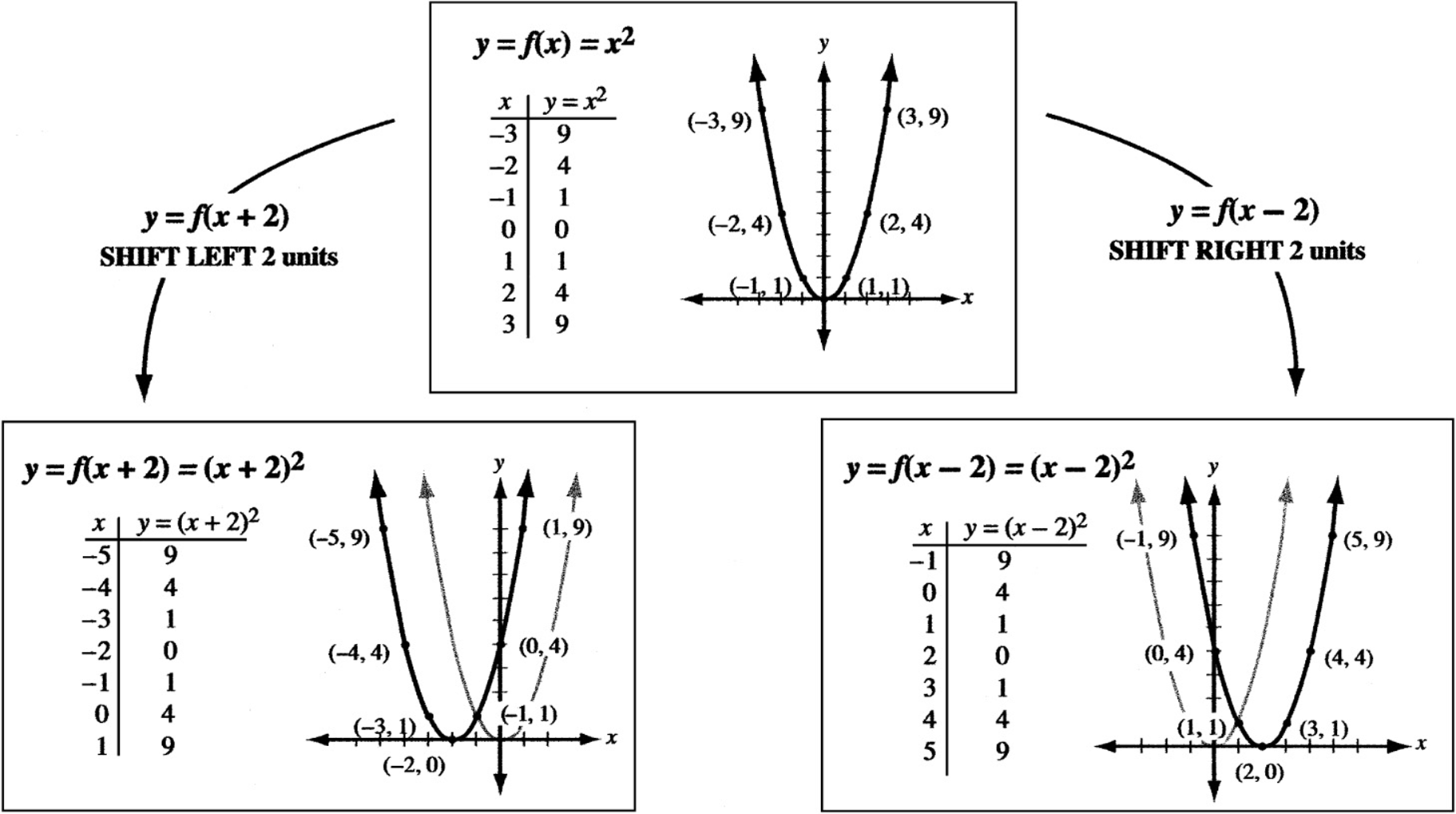
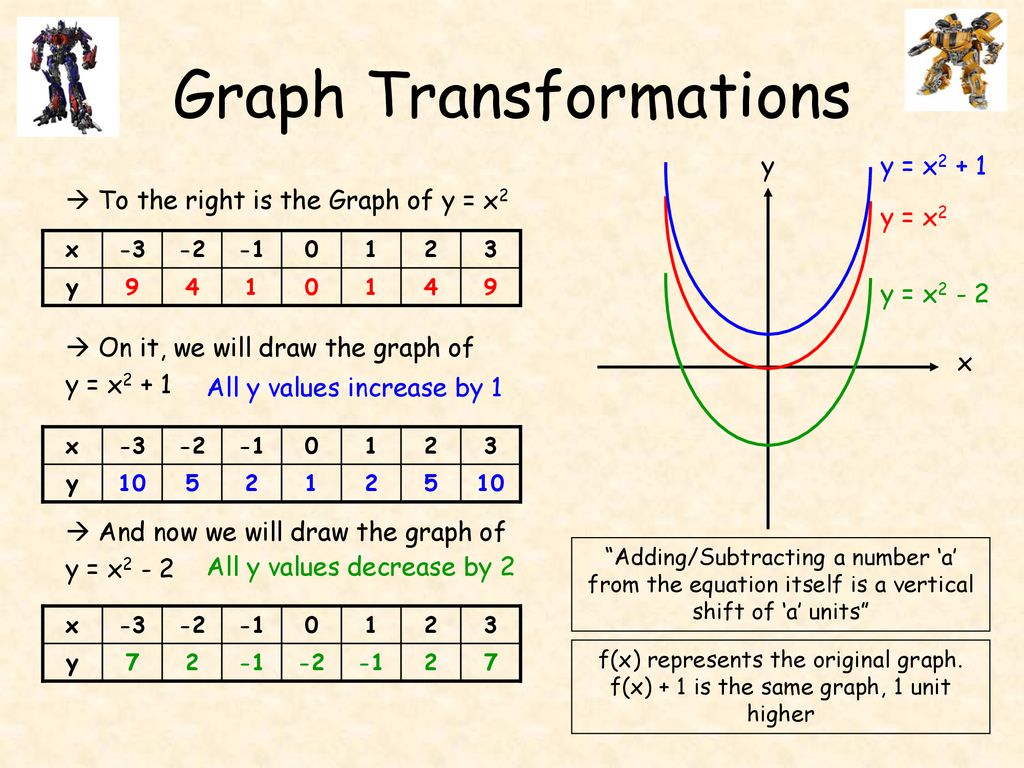
Now the graph of the function \(y = f(x 2)\) can be obtained from the graph of the original function \(f\) by translating each point on the graph \(2\) units to the left You might expect a shift to the right, but if you think that the \(y\) coordinate associated with \(x = 0\) on the old graph is now associated with \(x = 2\) on the newY = a f (x) b y = f (x) a c y = f (x a) d y = f (a x) Compositions of these transformations AM Understand how altering the values of m and c affects the graph of y = m x c AM84 Understand how altering the values of a, b and c in y = a (x b) 2 c affects the corresponding graphSection 56 Graphical Transformations In this section we are going to explore the graphical repercussions of alterations to a given function formula Specifically, we are going to explore how the graph of the function \(g\) compares to the graph \(f\) where

Graphing The Transformation Y F X H Concept Precalculus Video By Brightstorm
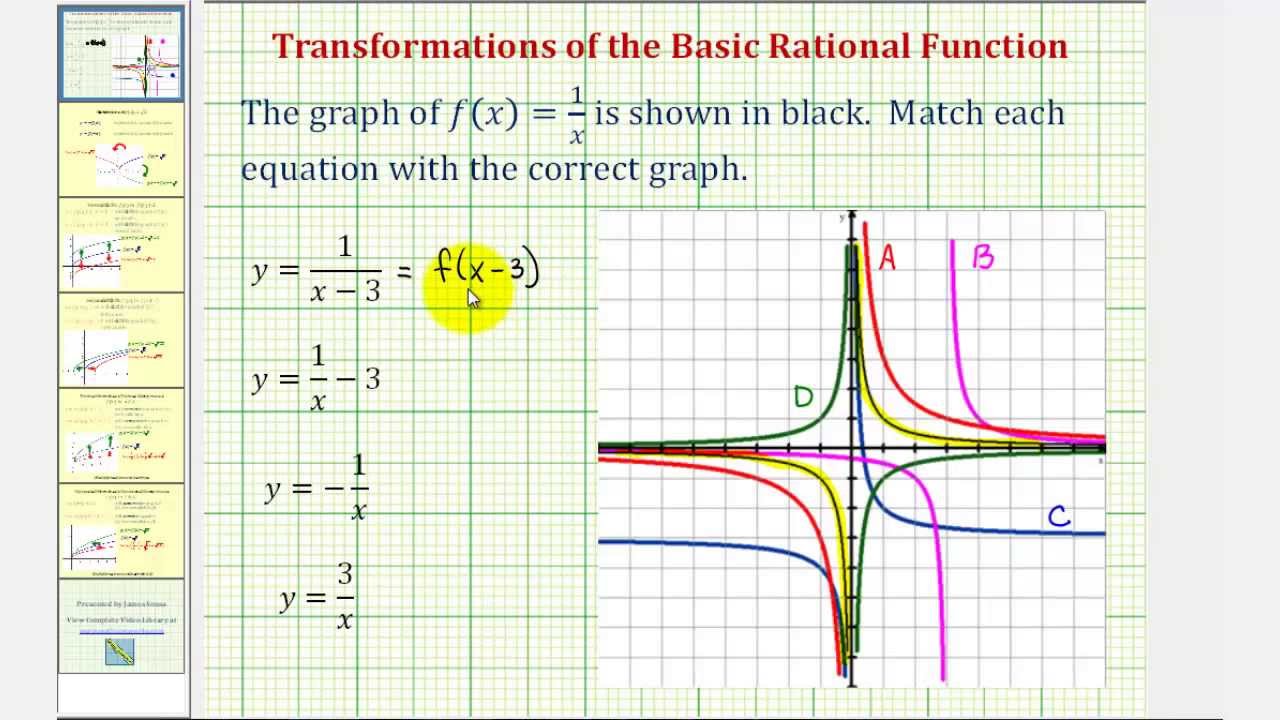
How to graph f(y)
How to graph f(y)-Graph Transformations There are many times when you'll know very well what the graph of a particular function looks like, and you'll want to know what the graph of a • Beginning with the graph f(x)=x2, we can use the chart on the previous page to draw the graphs of f(x 2),f(x 2), f(2x), f(1 2x), and f(x)Y = Cf(x) C > 1 stretches it in the ydirection;




Sketch The Graph Of The Function F X 2 X 1 3 Using Transformations Do Not Plainmath
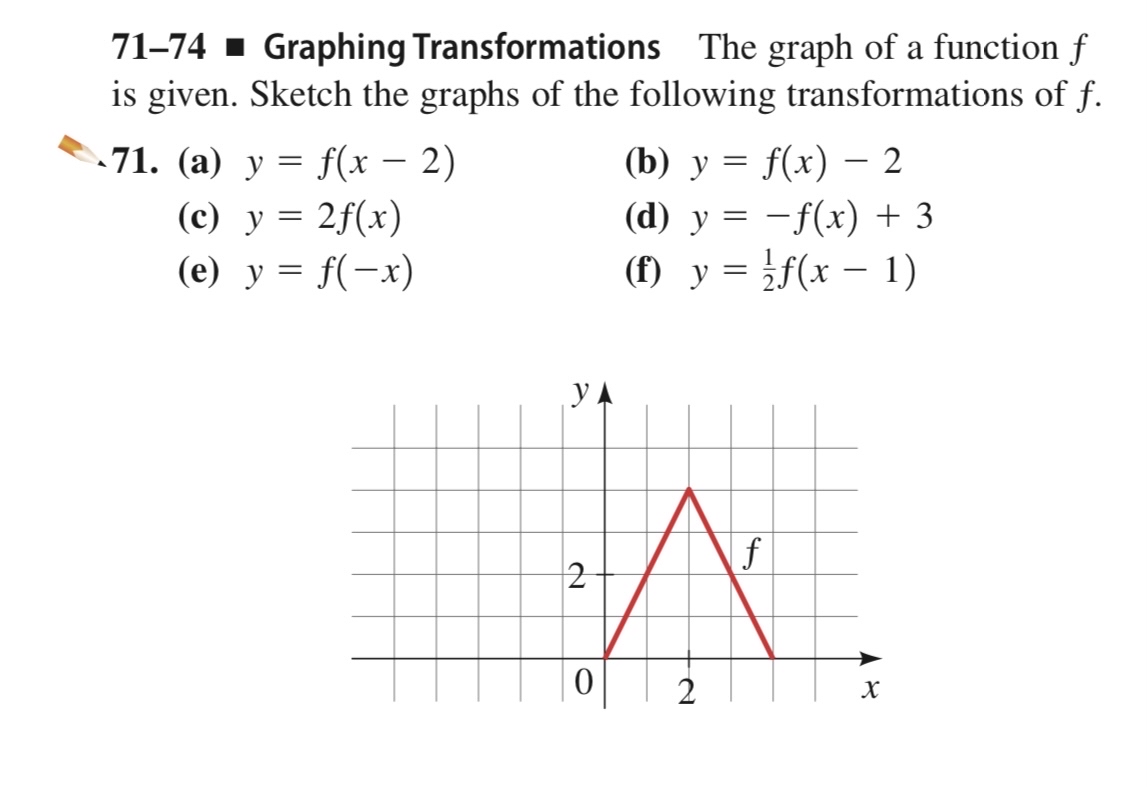
See the answer The graph of a function f is given Sketch the graphs of the following transformations of f (b) y = f (x) − 3 (c) y = 2f (x) (d) y = −f (x) 5 (e) y = f (−x) (f) y =1/2f (x − 4) Show transcribed image textAug 31, 15 · Describe the affects of the following graph transformations 𝑦=𝑓(𝑥10) Left 10 units 𝑦=3𝑓(𝑥) Stretch by factor of 3 on yaxis 𝑦=𝑓(2𝑥) Squash by factor of 2 on xaxis To what point will (4, 1) on the curve y = f(x) be transformed to under the following transformations?Transformation of curves Higher Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to
0 < C < 1 stretches it;The parent function is f(x) = cos(x) The following transformations have been applied a = 2 (Vertical stretch by a factor of 2) b = −1 (Reflection in the yaxis) h = 90° (Translation 90° to the right) k = 8 (Translation 8 units up) Practice Questions 1 The graph of f(x) = x3 was reflected in the yaxis, compressed vertically by a factor ofJan 21, 14 · 000 / 0 Live • Video tutorial on Graph Transformations y=3f (x) and y=f (2x) Tes classic free licence Report this resource to let us know if it violates our terms and conditions Our customer service team will review your report and will be in touch £000
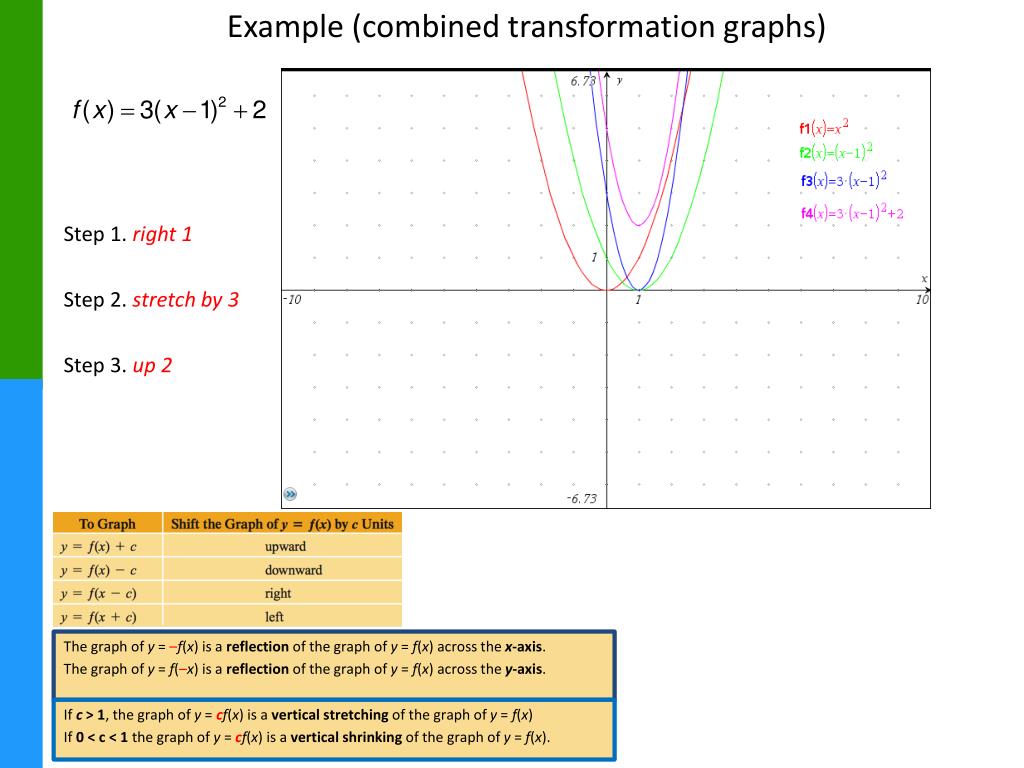
Transformations of Graphs Suppose we know what the graph of y f x looks like If c 0, then we can determine the graph that results when we define some new functions in terms of c, x, and f x Type of Transformation To Graph Do this to the graph of y f x0 < C < 1 compresses it;(ii) The graph y = f(−x) is the reflection of the graph of f about the yaxis (iii) The graph of y = f −1 (x) is the reflection of the graph of f in y = x Translation A translation of a graph is a vertical or horizontal shift of the graph that produces congruent graphs The graph of y = f(x c), c > 0 causes the shift to the left y



Graphing Reflections Y F X Or Y F X Youtube
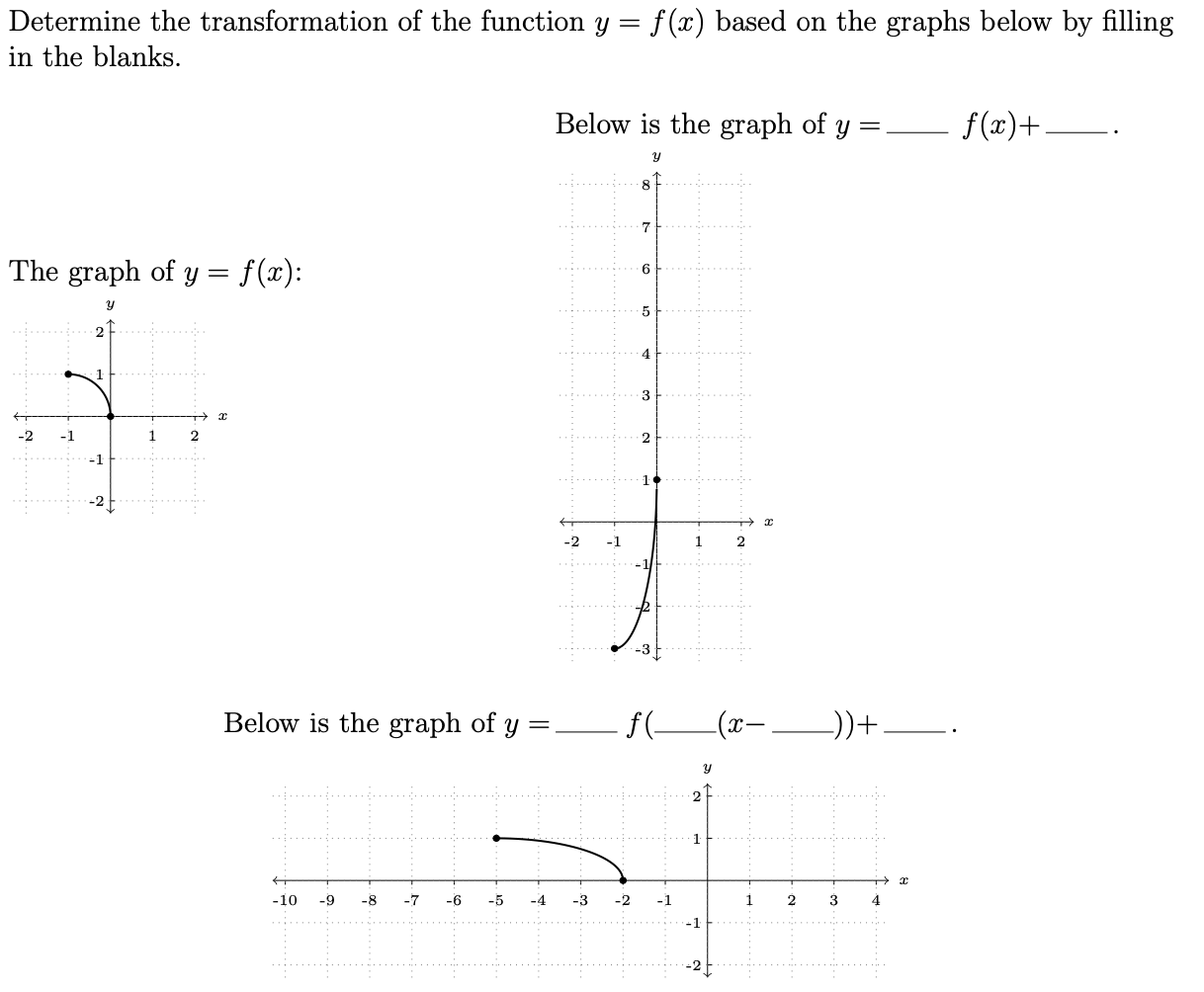



Solved Determine The Transformation Of The Function Y F Chegg Com
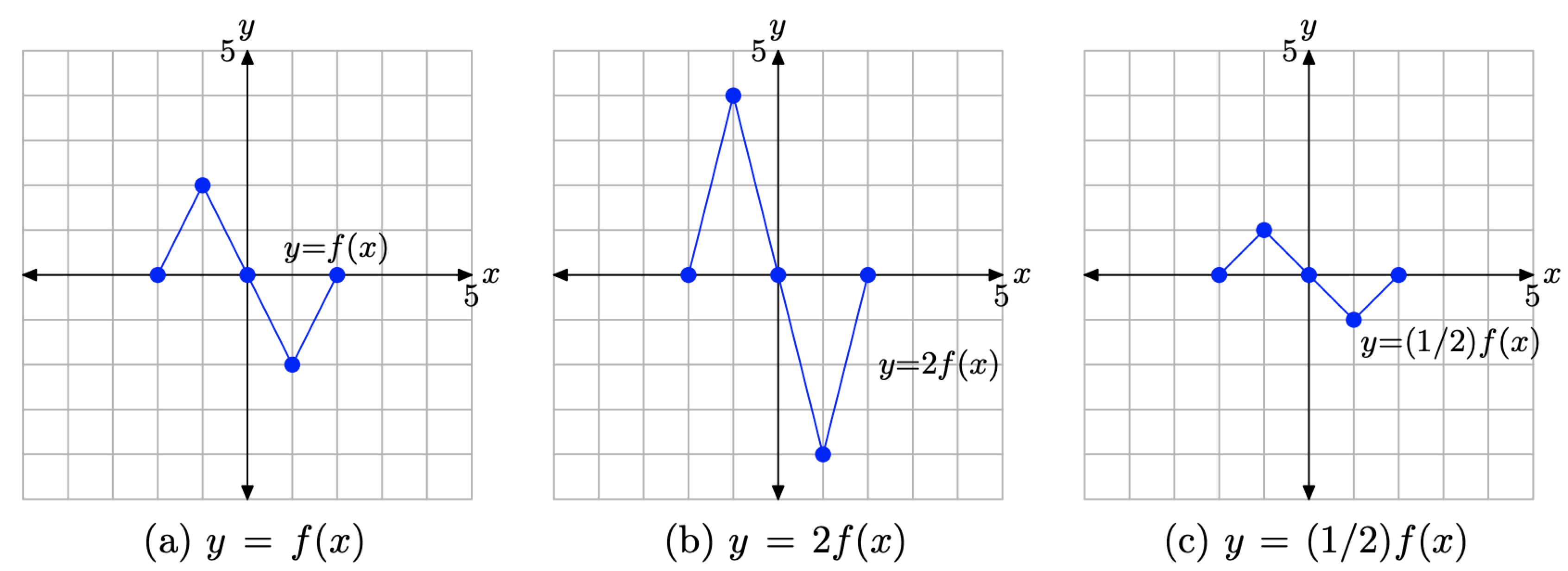
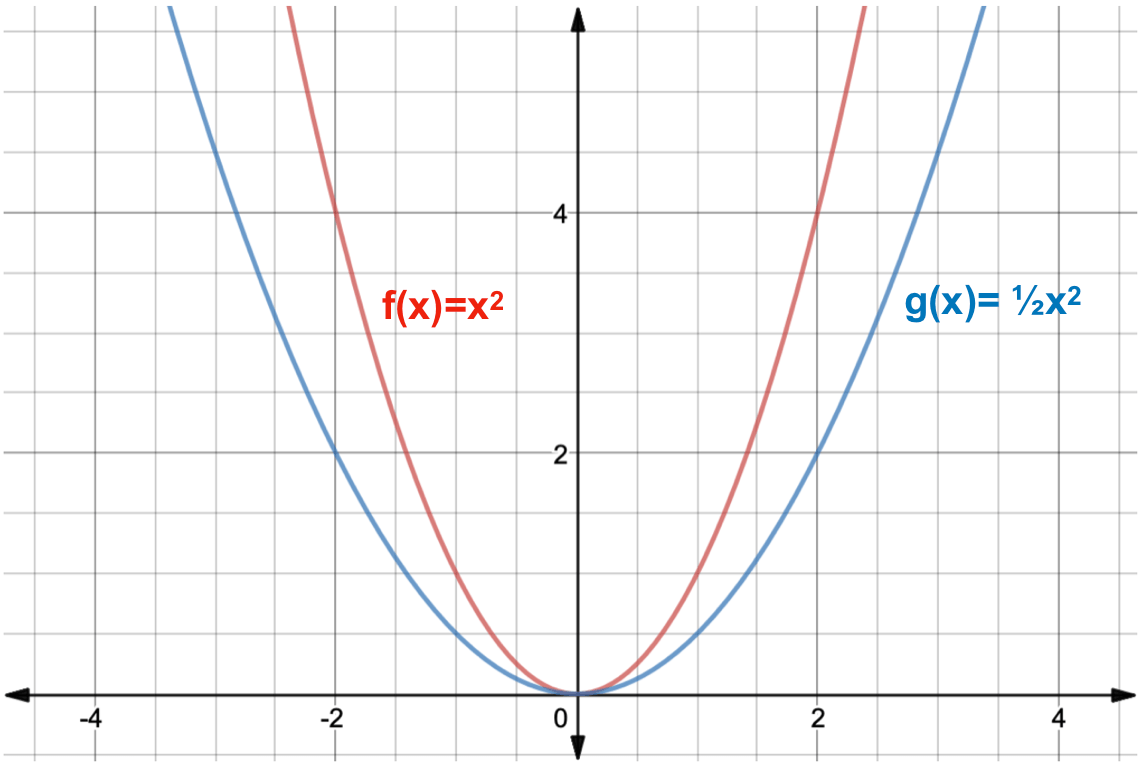
We can also stretch and shrink the graph of a function To stretch or shrink the graph in the y direction, multiply or divide the output by a constant 2f (x) is stretched in the y direction by a factor of 2, and f (x) is shrunk in the y direction by a factor of 2 (or stretched by a factor of ) Here are the graphs of y = f (x), y = 2f (x), andGraphic designers and 3D modellers use transformations of graphs to design objects and images Part of Maths y = f(x1) 1 10 Which function represents a reflection of the function f(xThe graph of y = f (x) is the graph of y = f (x) reflected about the yaxis Here is a picture of the graph of g(x) =(05x)31 It is obtained from the graph of f(x) = 05x31 by reflecting it in the yaxis Summary of Transformations To graph Draw the graph of f and Changes in the equation of y = f(x) Vertical Shifts y = f (x) c
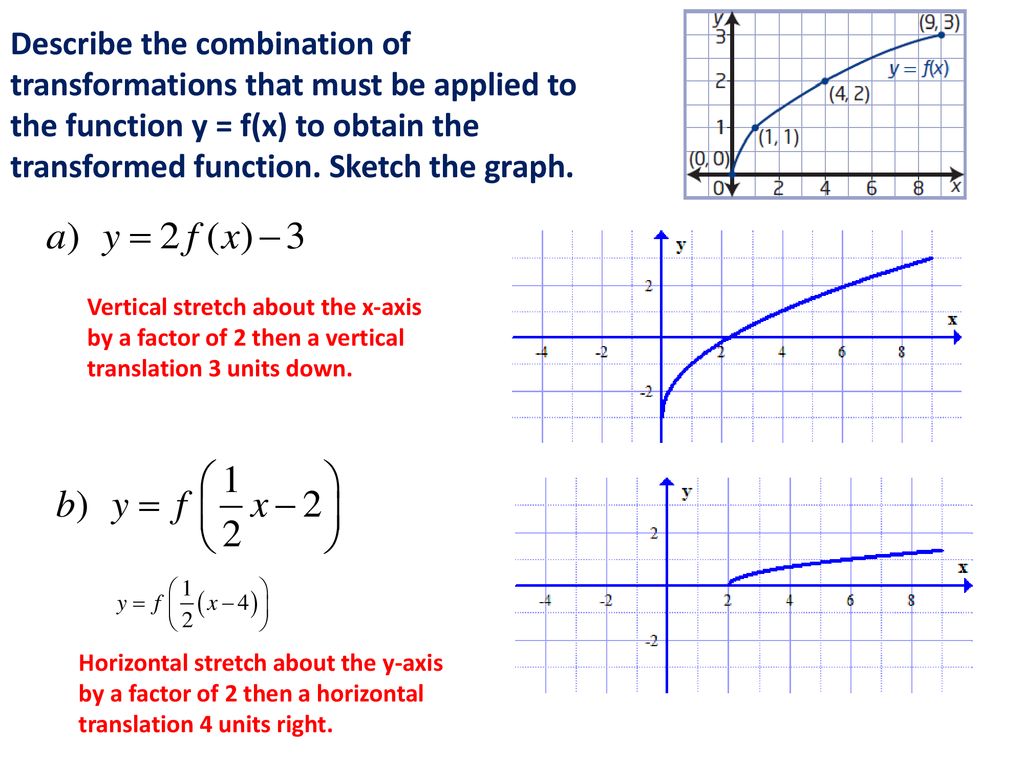



1 3 Combining Transformations Ppt Download



How To Reflect A Graph Through The Y Axis Studypug
Each output variable has one or more input variables that are represented by the letter X The process transforms the X input variables into a Y output variable The equation is written as Y = f (X), and we understand this to mean that the output of a process is a function of the inputsGraphing the Transformation y = f(−x), Reflective Transformation There are different types of transformations and their graphs, one of which is a math reflection across the yaxis If we get the same function from a math reflection, it is a symmetrical function, specifically even A math reflection flips a graph over the yaxis, and is of theWhen you are dealing with transforming graphs, you can translate, reflect and stretch, enlarging in one direction, but not rotation In this activity, we are going to look at stretching vertically y = f(x) → y = af(x) This does like quite daunting at first but it is actually quite intuitive




Reflections Of Trig Graphs Examsolutions
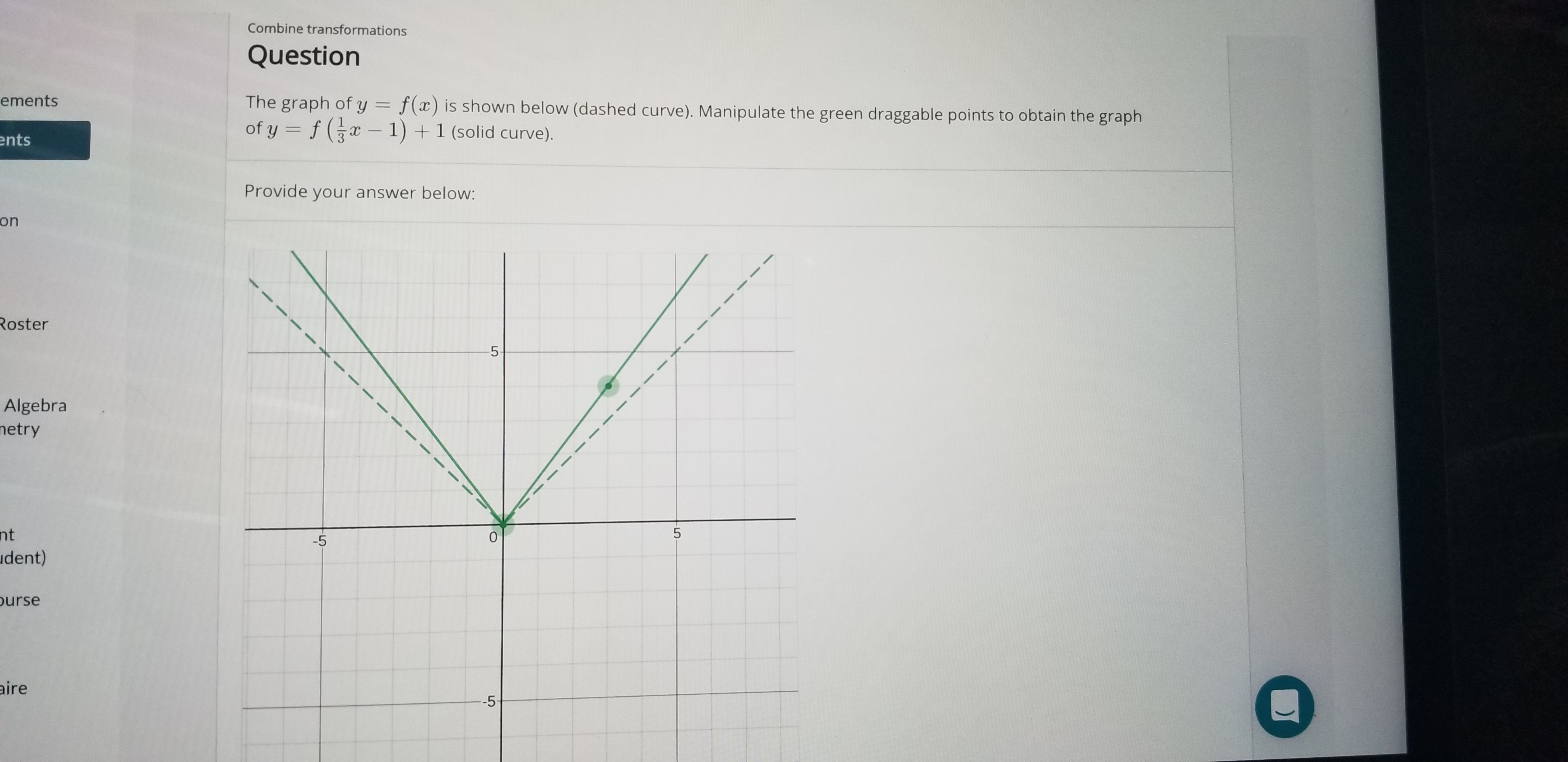



Answered Combine Transformations Question The Bartleby
Nov 02, 18 · Graph Transformations Author hnees Topic Function Graph Absolute Value Transformations Exponential Parent Function Transformation of Logarithms Exploring Quadratic Functions Functions transformationssquare root, quadratic, abs value Position vs time graphs controlling velocity;Mar 02, 18 · You also have y = f (2x) Where does the point (2, 4) move to on the new graph?The graph transformation rules are very helpful not just in graphing but also in analyzing the behavior of the graphs Answer and Explanation 1 We are given the function {eq}f(x) {/eq}




Graphing The Transformation Y F X H Concept Precalculus Video By Brightstorm




Sketch The Graph Of The Function F X 2 X 1 3 Using Transformations Do Not Plainmath
Graphs and Transformations wwwnaikermathscom Graphs and Transformations Edexcel Past Exam Questions 2 1 Figure 1 Figure 1 shows a sketch of the curve C with equation y = f(x), where f(x) = x2(9 – 2x)There is a minimum at the origin, a maximum at the point (3, 27) and C cuts the xaxis at the point A (a) Write down the coordinates of the point AC < 0 moves it down;Mar 07, · IBDP Past Year Exam Questions – Transformation Q1 N10P2 The diagram shows the graph of a linear function and a quadratic function On the same axes sketch the graph of f g Indicate clearly where the x intercept and the asymptotes occur 5 marks Q2 M08P2TZ2 The graph of y = f x for – 2 ≤ x ≤ 8 is shown



Trasformations By Graph Paper Teacher Guide
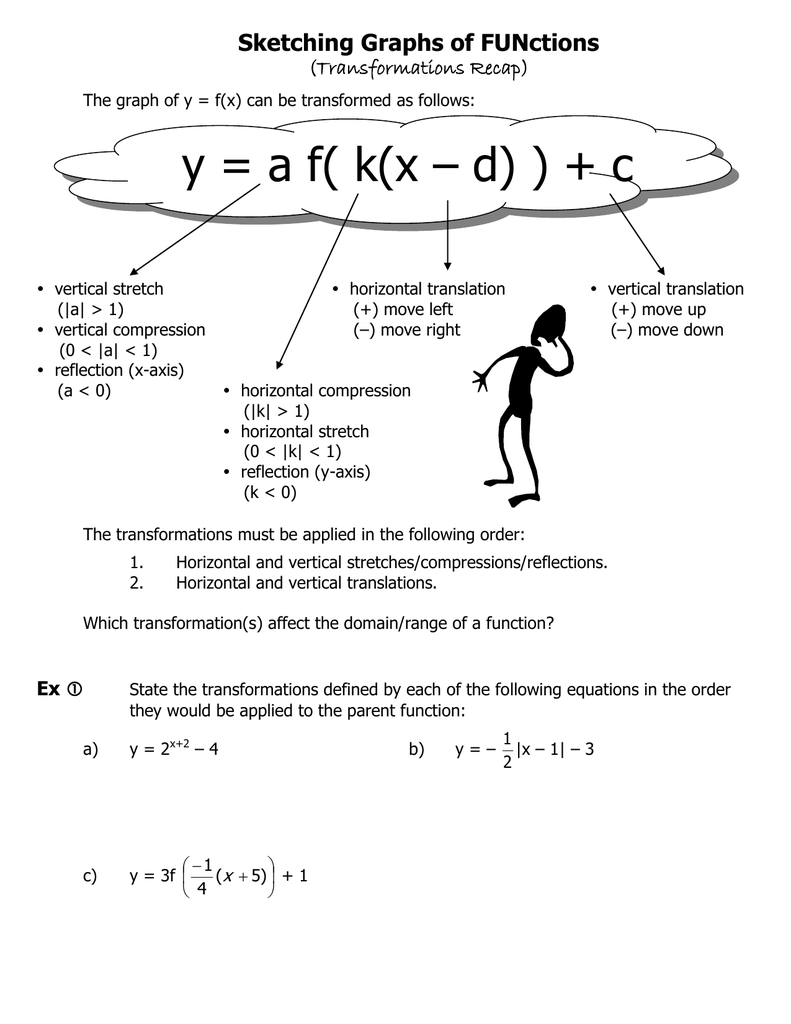



Y A F K X D C
(ii) The graph y = f(−x) is the reflection of the graph of f about the yaxis (iii) The graph of y = f −1 (x) is the reflection of the graph of f in y = x Translation A translation of a graph is a vertical or horizontal shift of the graph that produces congruent graphs The graph of y = f(x c), c > 0 causes the shift to the left yGraph transformations Given the graph of a common function, (such as a simple polynomial, quadratic or trig function) you should be able to draw the graph of its related functionC < 0 moves it right;




Reflect Function About Y Axis F X Expii
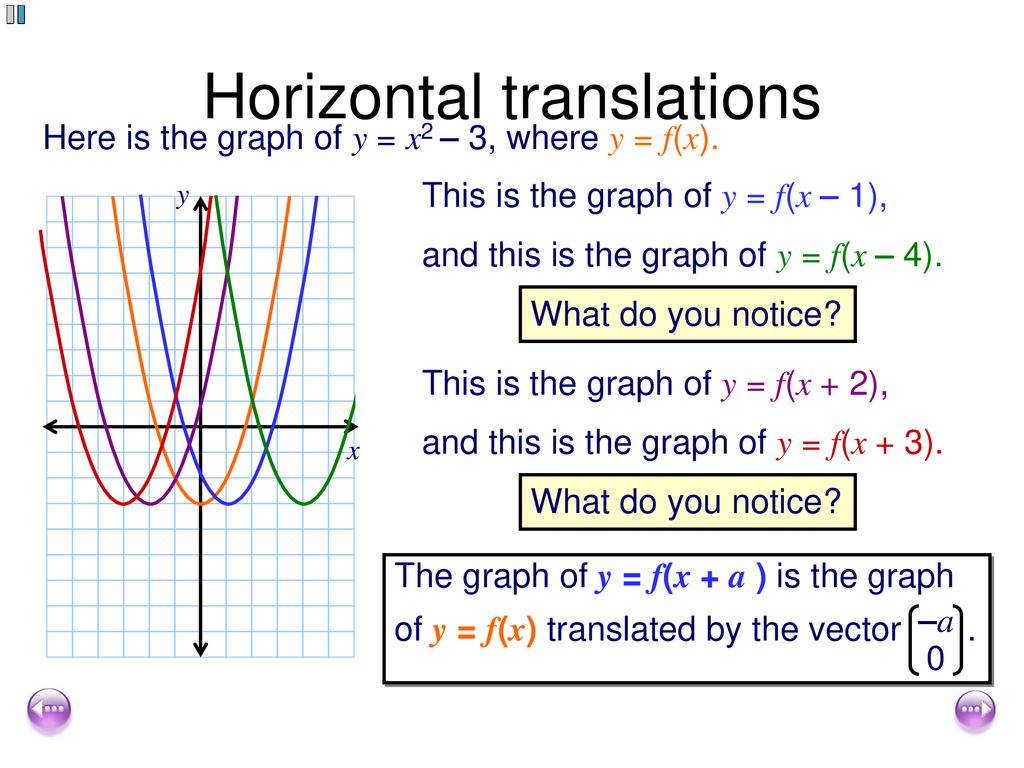



Transforming Graphs Of Functions Ppt Download
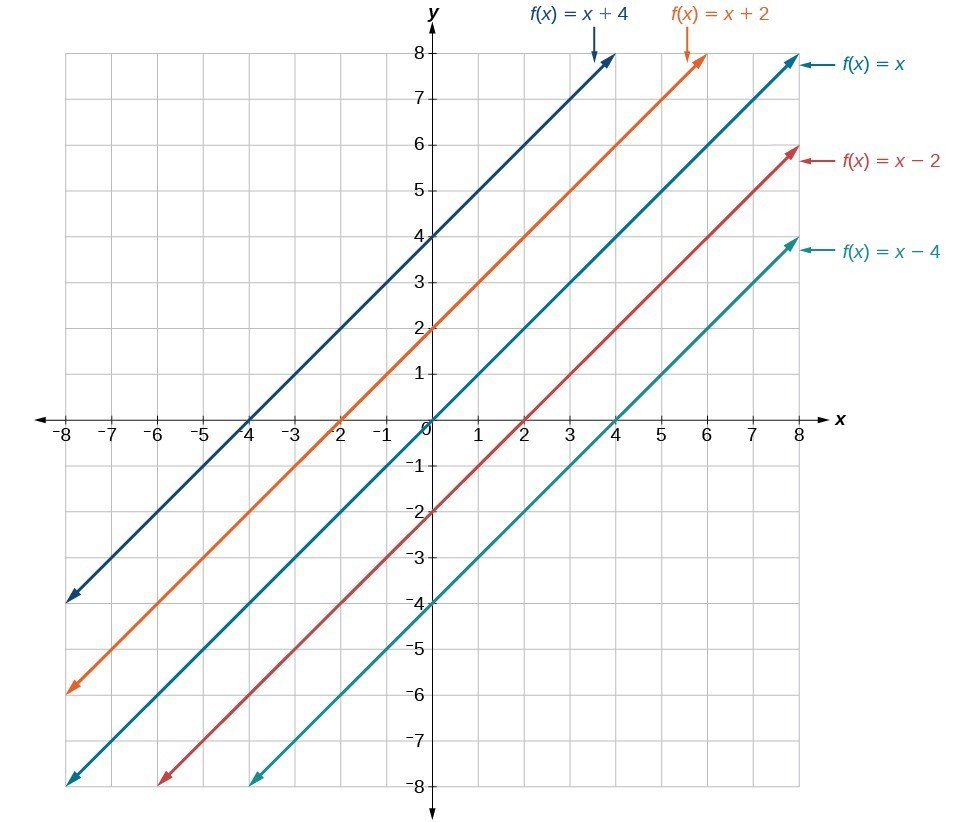
1) (−1,2) 2)(−1,−8) 3)(4,−3) 4)(−6,−3)Y = f(x C) C > 0 moves it left;Graph the transformations below by doing the following on graphing paper • Graph the basic function used in this transformation (Example f(x) = x2) Use your Library of Functions Handout if necessary • State the series of transformations and the order in which they occur • Graph the transformation




Horizontal And Vertical Graph Stretches And Compressions Video Lessons Examples And Solutions




Mystery Transformation Reflections In The Why
Well you know if you put in 2 into the function you will receive 4 as a value of y So now you can "solve" for the new X coordinate 2x = 2, so x = 2/2 = 1 From this it's very intuitive to see why you stretch by 1/2 Think of it as solving an equationThat is, the rule for this transformation is –f (x) To see how this works, take a look at the graph of h(x) = x 2 2x – 3Tan(x) & Unit Circle Degrees




Identifying Function Transformations Video Khan Academy




Shifting Functions Examples Video Khan Academy
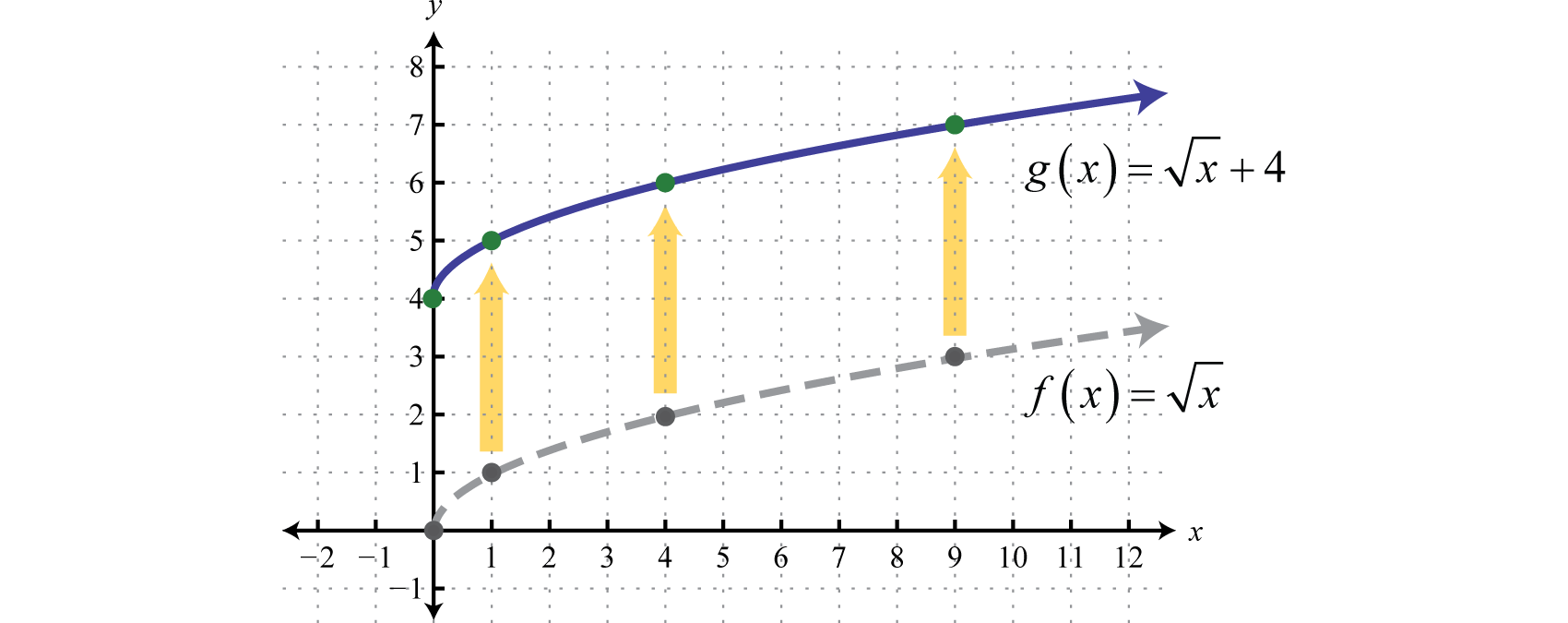
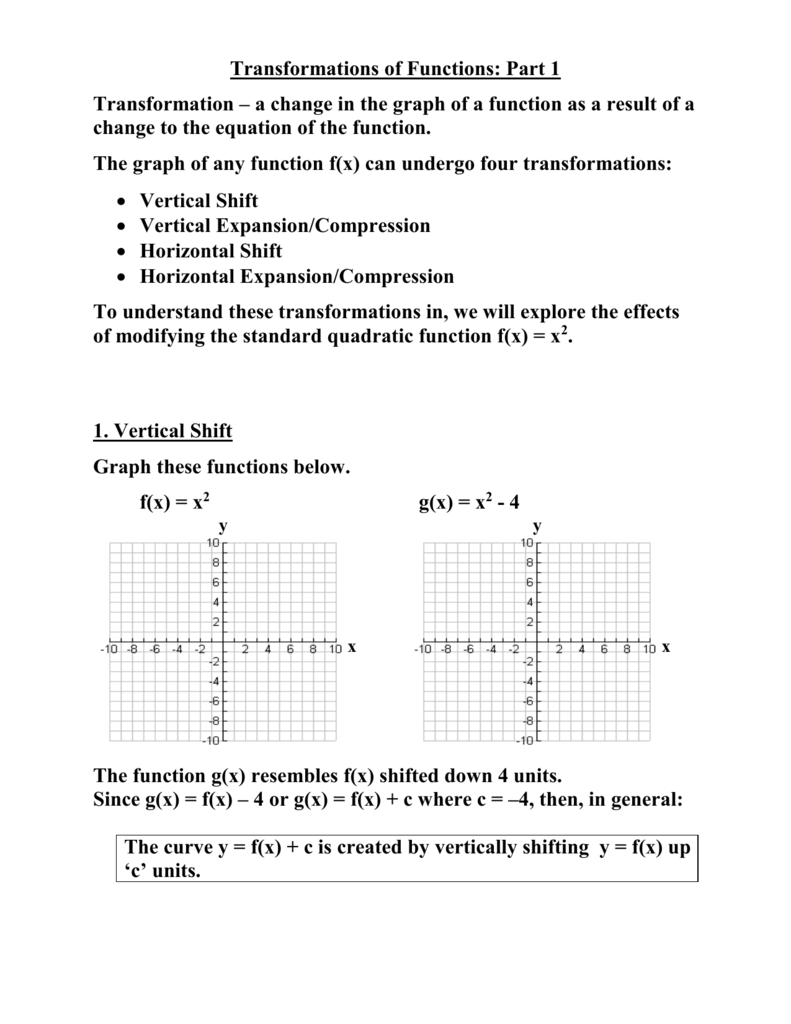
Question 10 < If the graph of y = f(x) is known, then the graph of y = f(26) 8 moves the graph off by the transformations of reflect over xaxis, left 6 units, down 8 units reflect over yaxis, right 6 units, down 8 units reflect over xaxis, right 6 units, down 8 units reflect over yaxis, left 6 units, down 8 units reflect over originStarting at y=2f(x), click on the circle to reveal a new graph Describe the transformation Click again to remove and try the next functionJan 02, 21 · To graph \(y=f(x)k\), shift the graph of \(y=f(x)\) up \(k\) units by adding \(k\) to the \(y\)coordinates of the points on the graph of \(f\) To graph \(y=f(x)k\), shift the graph of \(y=f(x)\) down \(k\) units by subtracting \(k\) from the \(y\)coordinates of the points on the graph



Vce School Notes Graph Transformations
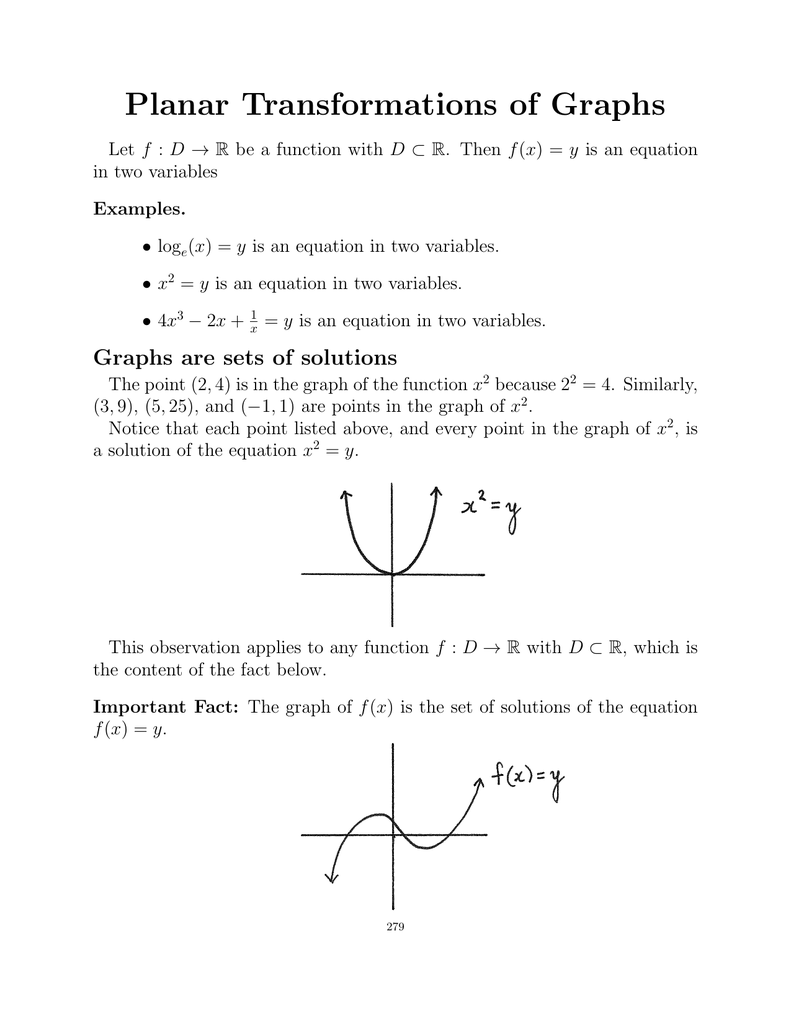



Planar Transformations Of Graphs F X F
In this video you are shown how the function y=f(axb) transforms the graph of y=f(x) as a combination of stetches and translations parallel to the xaxis IY = f(x) C C > 0 moves it up;Aug 15, 13 · so this red curve is the graph of f of X and this blue curve is the graph of G of X and I want to try to express G of X in terms of f of X and so let's see how they're related so we pick any X and we could start right here at the vertex of f of X and we see that at least at that point G of X is exactly one higher than that so G of two I could write this down G of two G of two is equal to is



Question Video Identifying The Coordinates Of Points Following A Transformation Nagwa



Using Transformations To Graph Functions
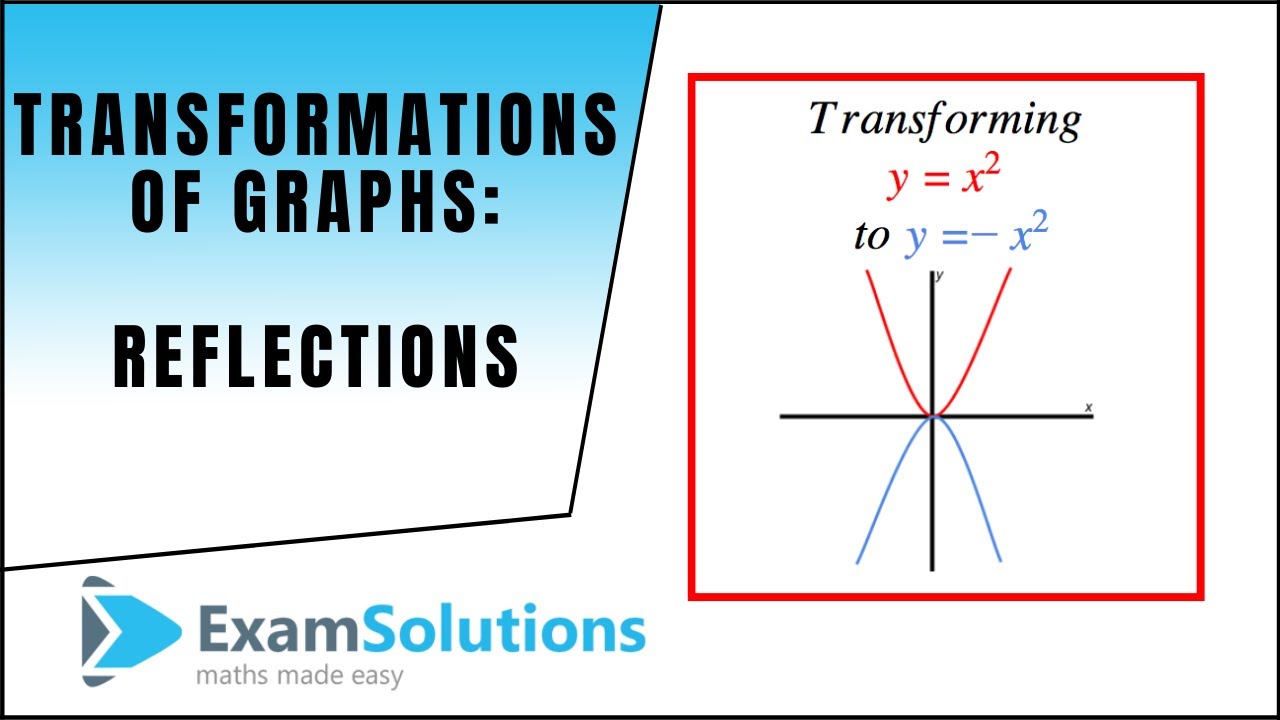
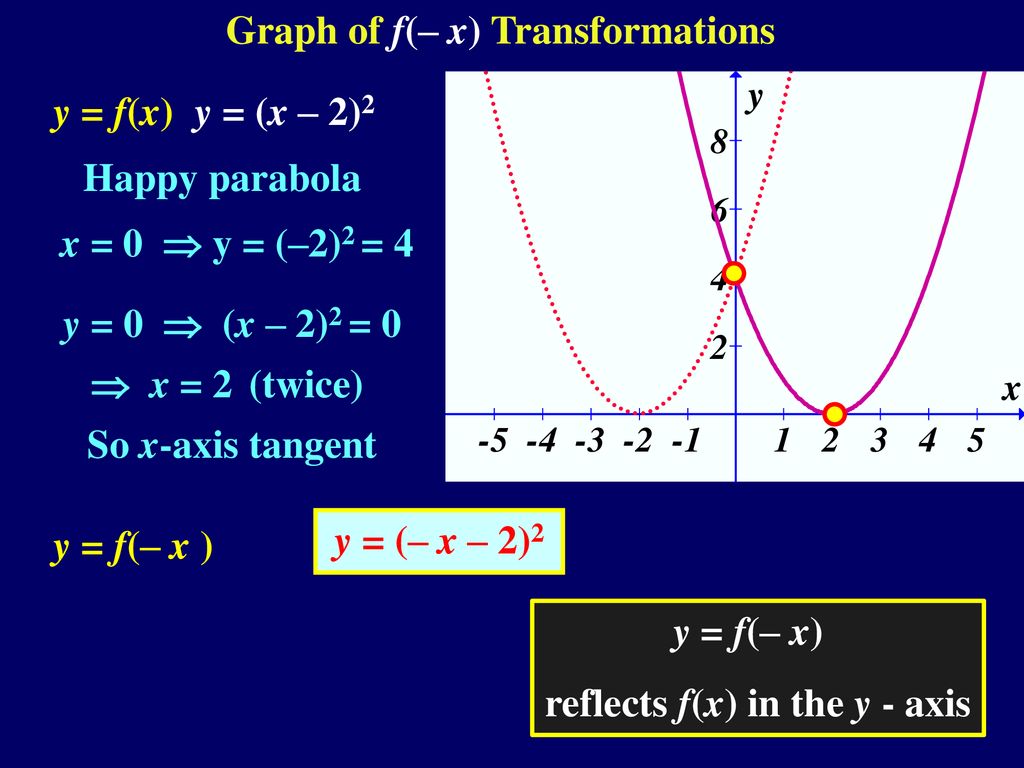
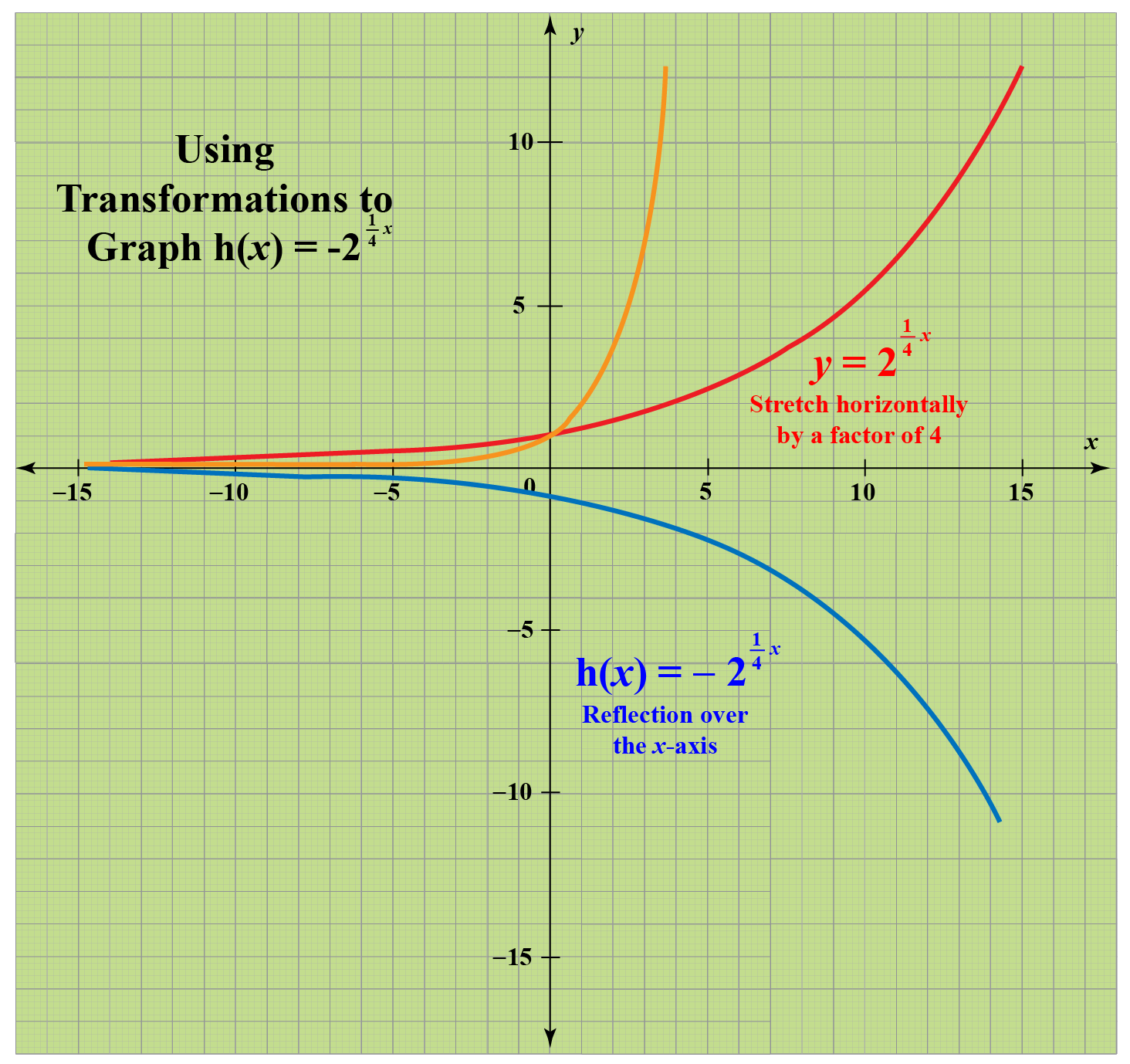
Purplemath The last two easy transformations involve flipping functions upside down (flipping them around the xaxis), and mirroring them in the yaxis The first, flipping upside down, is found by taking the negative of the original function;Geometric Transformations of Functions We start with a java applet to explore graphically the basic geometric transformations of functions We now proceed to express these geometrical transformations in algebraic terms Translations of Functions Suppose that y = f (x) is a function and c > 0;Y = −f(x) Reflects it about xaxis;




Using Transformations To Graph Functions



Trigonometric Function Transformations Degrees Geogebra
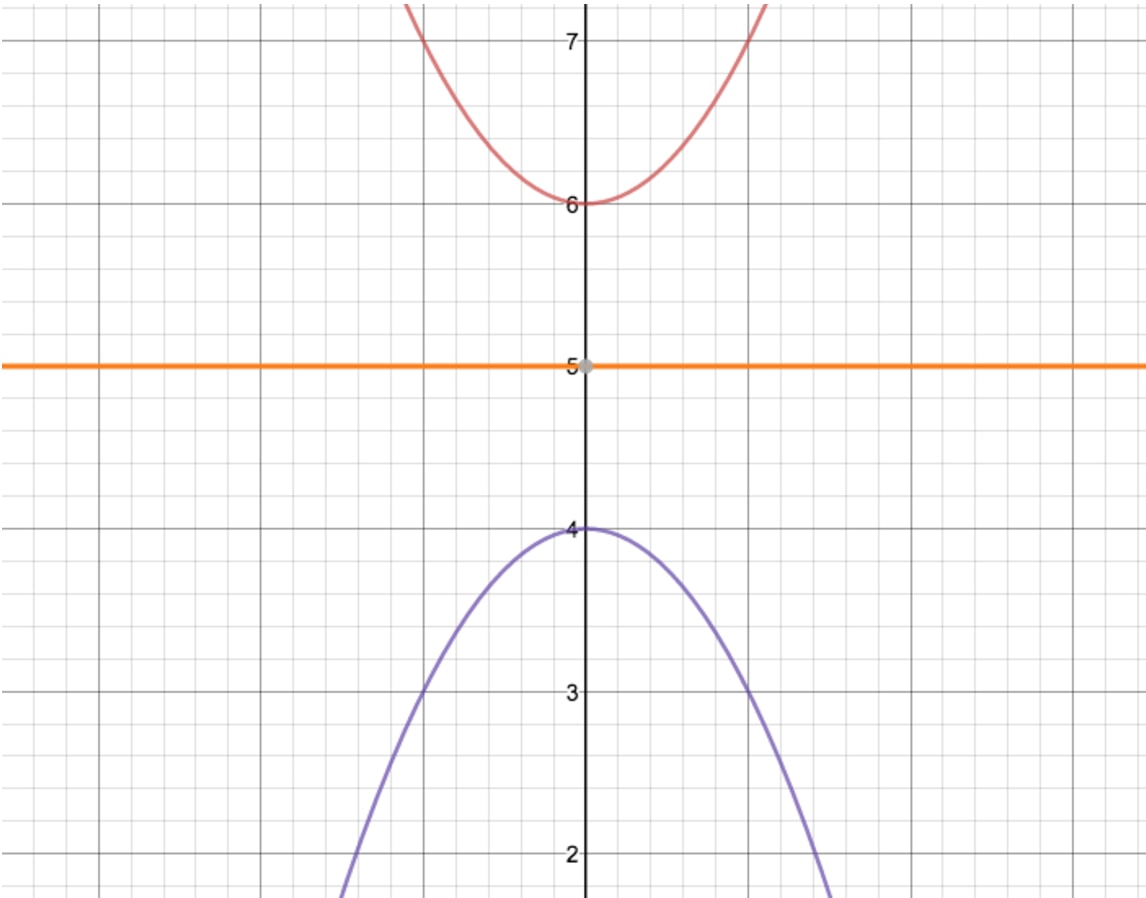
The y intercept of the graph y = 1 f ( x) is given by 1 f ( 0), which is the reciprocal of y 0 Similarly, the old horizontal asymptote, y = lim x → ∞ f ( x) = 2, will become y = lim x → ∞ 1 f ( x) = 1 lim x → ∞ f ( x) = 1 2, since f ( x) is being replaced by 1 f ( x)Y = f(Cx) C > 1 compresses it in the xdirection;Y = f (x) becomes y = f (x ± a) These transformations are called horizontal shifts or translations They move the graph of the given function left (adding positive a) or right (subtracting positive a) The parameter a can multiply the input x before the rule f is applied



Transformations Of Graphs Reflections Y F X F X Examsolutions Youtube



Vce School Notes Graph Transformations
Use transformations of graphs to sketch a graph of y=f(x) by hand Do not use a calculator f(x)=\sqrt{1x} 🚨 Hurry, space in our FREE summer bootcamps is running out 🚨 Claim your spot hereMultiplying a function by a negative constant, − f (x), reflects its graph in the xaxis Multiplying the values in the domain by −1 before applying the function, f (− x), reflects the graph about the yaxis When applying multiple transformations, apply reflections first1) y=f(x7)−3 2)y=f(x7)3 3)y=f(x−7)−3 4)y=f(x−7)3 2 The minimum point on the graph of the equation y=f(x) is (−1,−3) What is the minimum point on the graph of the equation y=f(x) 5?
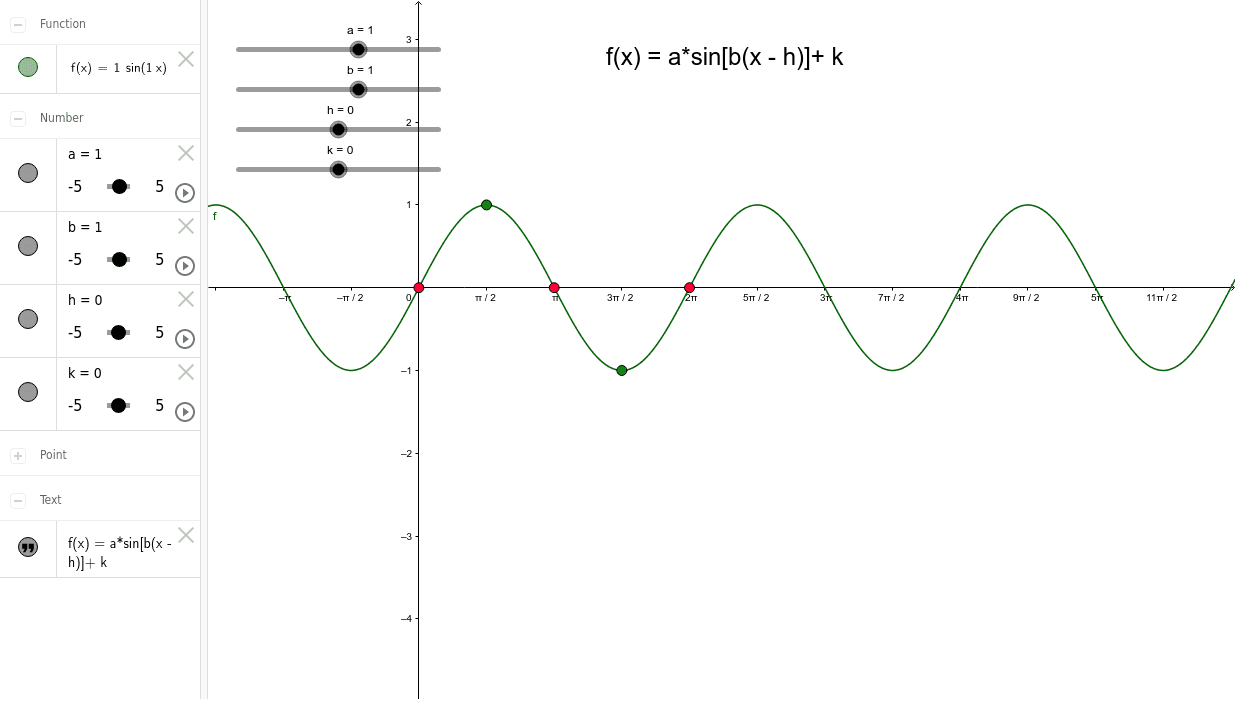



Sine Graph Transformations Geogebra




Transformation Of Graph Y F X Into Y F X And Y F
Then the graph of y = f (x c) is obtained by1 Which transformation of y=f(x) moves the graph 7 units to the left and 3 units down?Dec 09, 19 · y=f (x) will indicate that the graph has reflected about the yaxis y=f (x) will indicate that the graph has reflected about the origin If I have f (x)= (x) 3, then the graph would be reflected about the yaxis Try to experiment on these transformations by using a graphing utility such as Desmos, Symbolab, GeoGebra




Section 1 3 Transformations Of Graphs Pdf Free Download
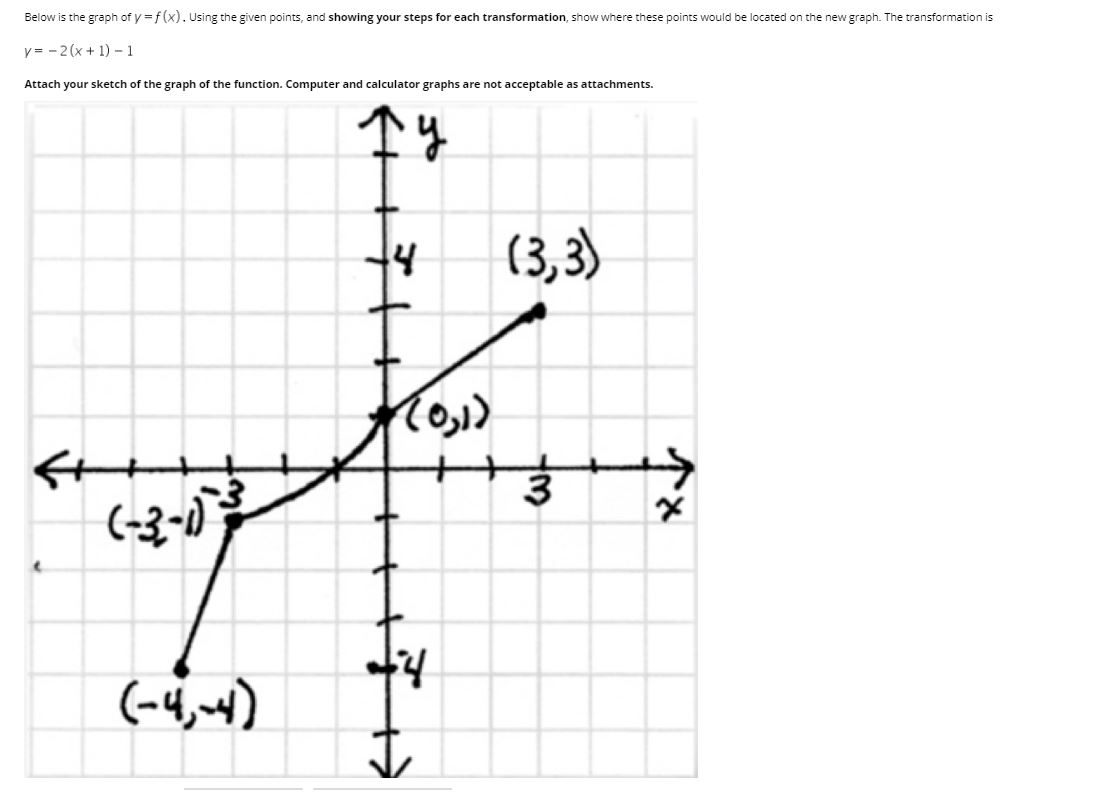



Solved Below Is The Graph Of Y F X Using The Given Poin Chegg Com
Transcribed image text (5 points each) The graph of y = f(x) is given below Perform the transformations to obtain y = f(23) 4 (a) In words, state the transformations done to y = f(x) List the transformations in the order they occurAug 29, 17 · A horizontal translation 60 is a rigid transformation that shifts a graph left or right relative to the original graph This occurs when we add or subtract constants from the \(x\)coordinate before the function is applied For example, consider the functions defined by \(g(x)=(x3)^{2}\) and \(h(x)=(x−3)^{2}\) and create the following tablesTutorial on transformations of graphs and more specifically, reflections on the xaxis and yaxisYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXA
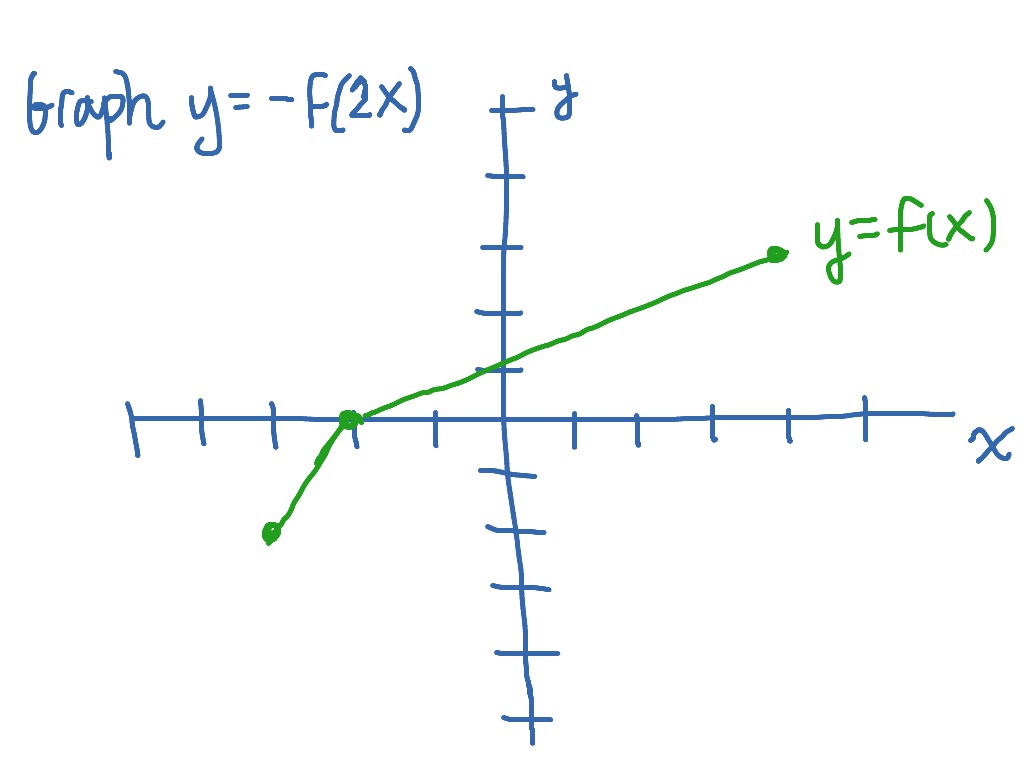



Graphing Y F 2x As A Transformation Of Y F X Math Showme



Reflect Function About Y Axis F X Expii
Y = f(−x) Reflects it about yaxis
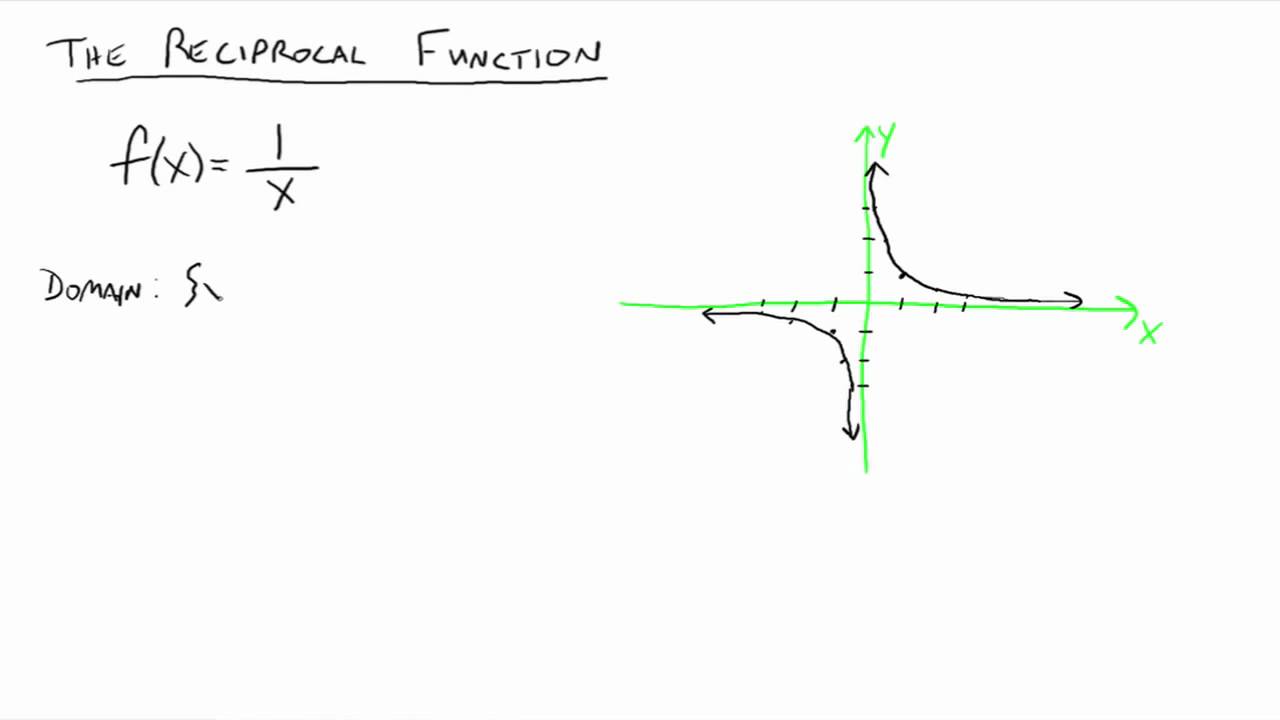



Graphs Of Reciprocal Functions Video Lessons Examples And Solutions
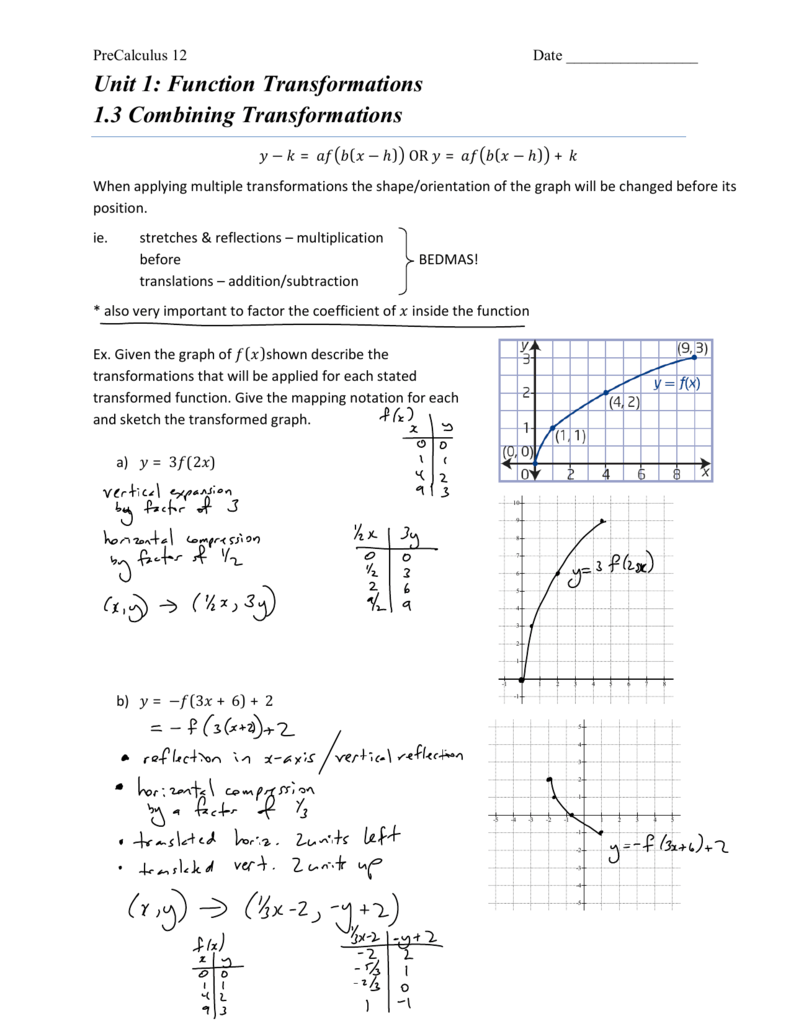



Unit 1 Function Transformations 1 3 Combining Transformations
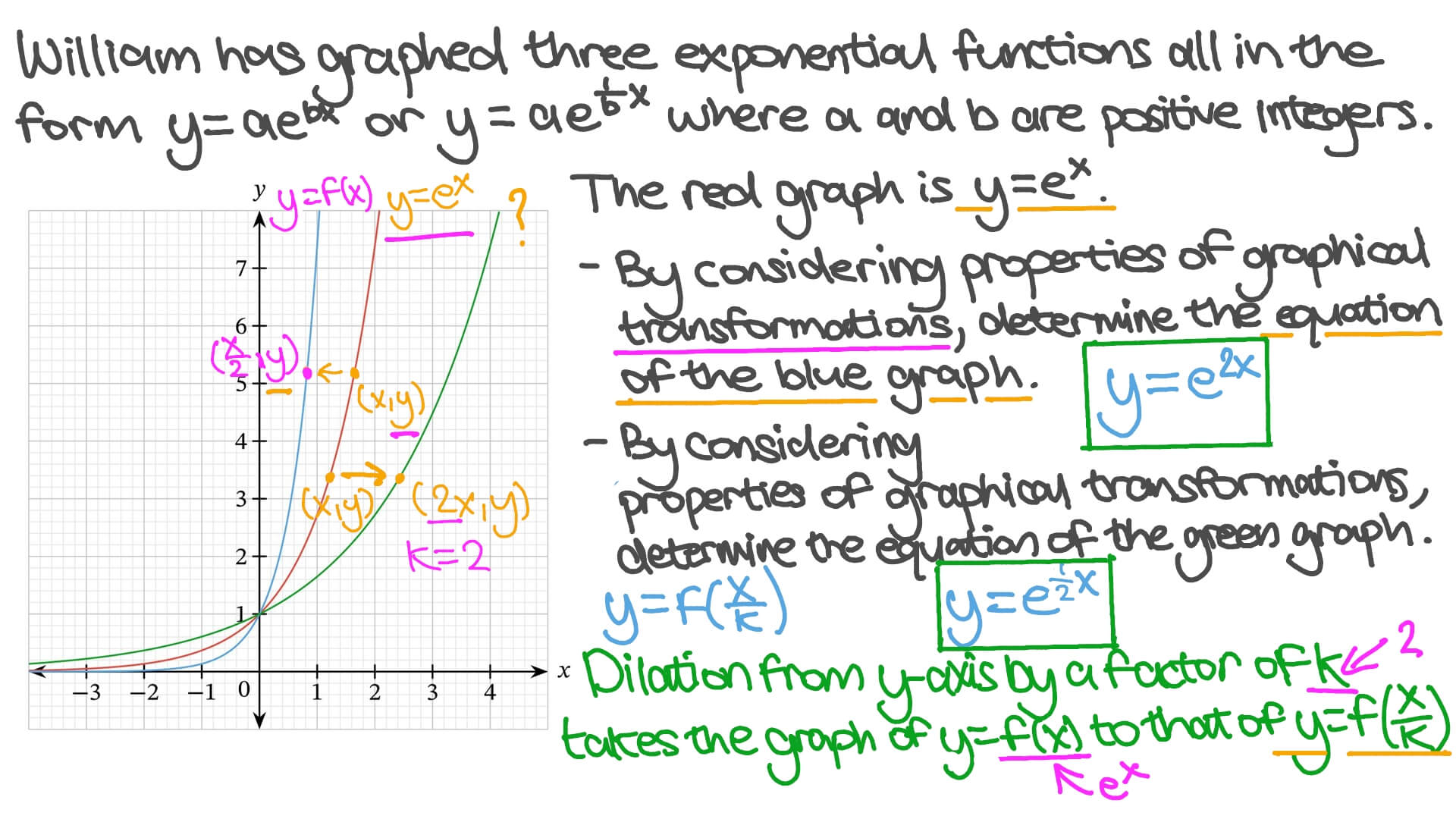



Question Video Graph Transformations Of Exponential Functions Nagwa



Practice Questions Transformation Ibdp Math Hl Sl



Transformation Of Graphs Translations




Transforming Graphs Of Modulus Functions Youtube
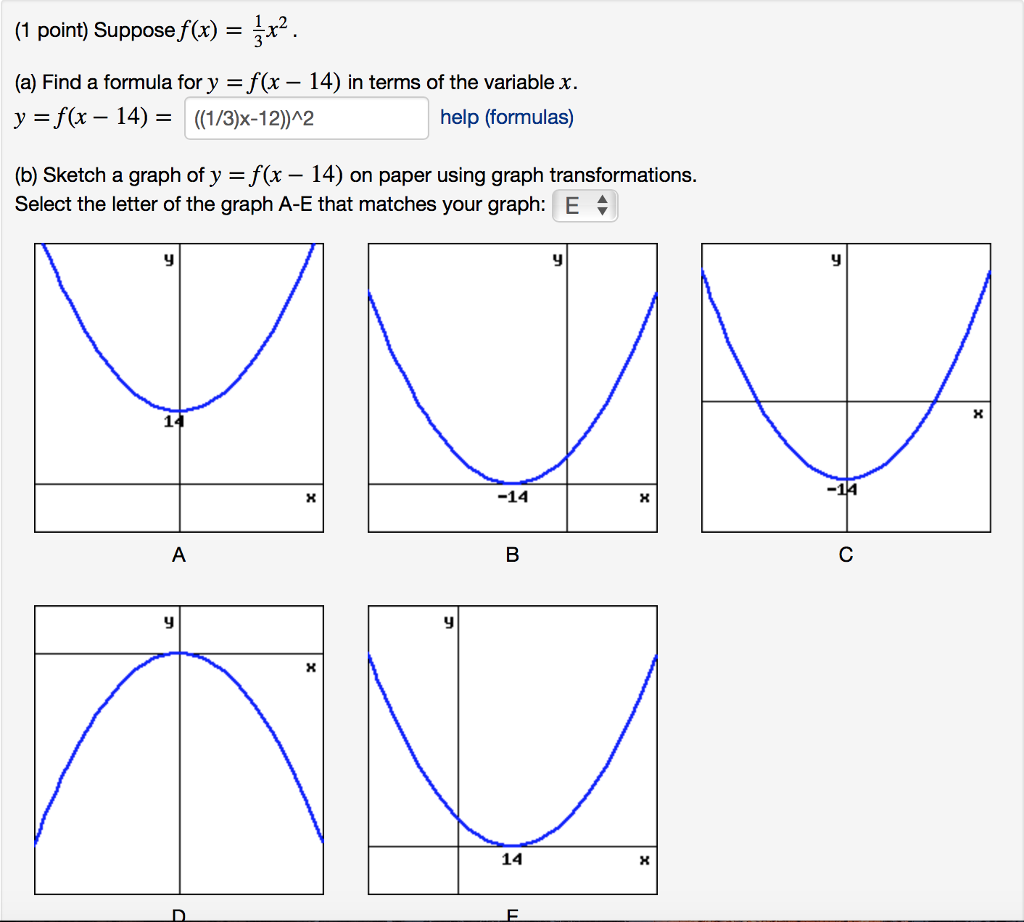



Suppose F X 1 3 X 2 A Find A Formula For Y Chegg Com
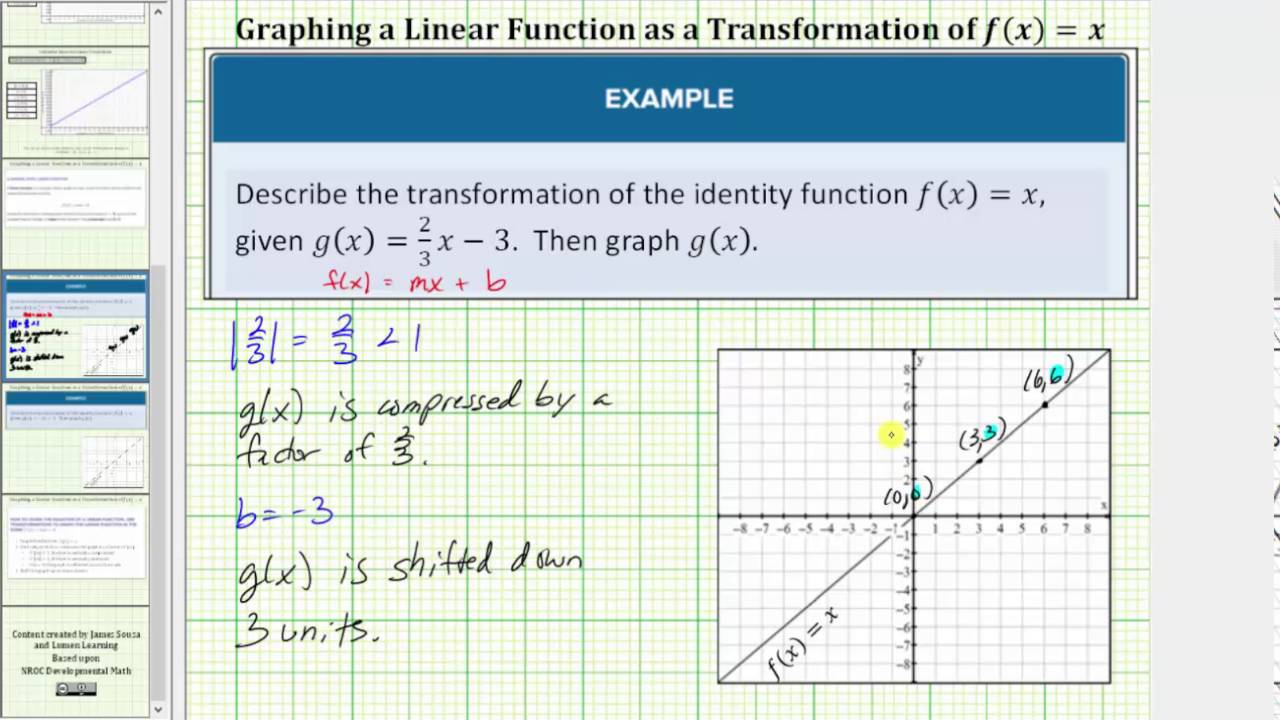



Read Transform Linear Functions Intermediate Algebra



Part 1 The Graph Of Fx Is Shown It Goes Through Gauthmath




Urgent Use A Table To Compress The Function Y F X Vertically By 1 2 Identify The Graph Of The Brainly Com



The Graph Of Y H X Is A Transformation Of The Graph Of Y G X Steps Please Thank You Socratic



Read Transform Linear Functions Intermediate Algebra
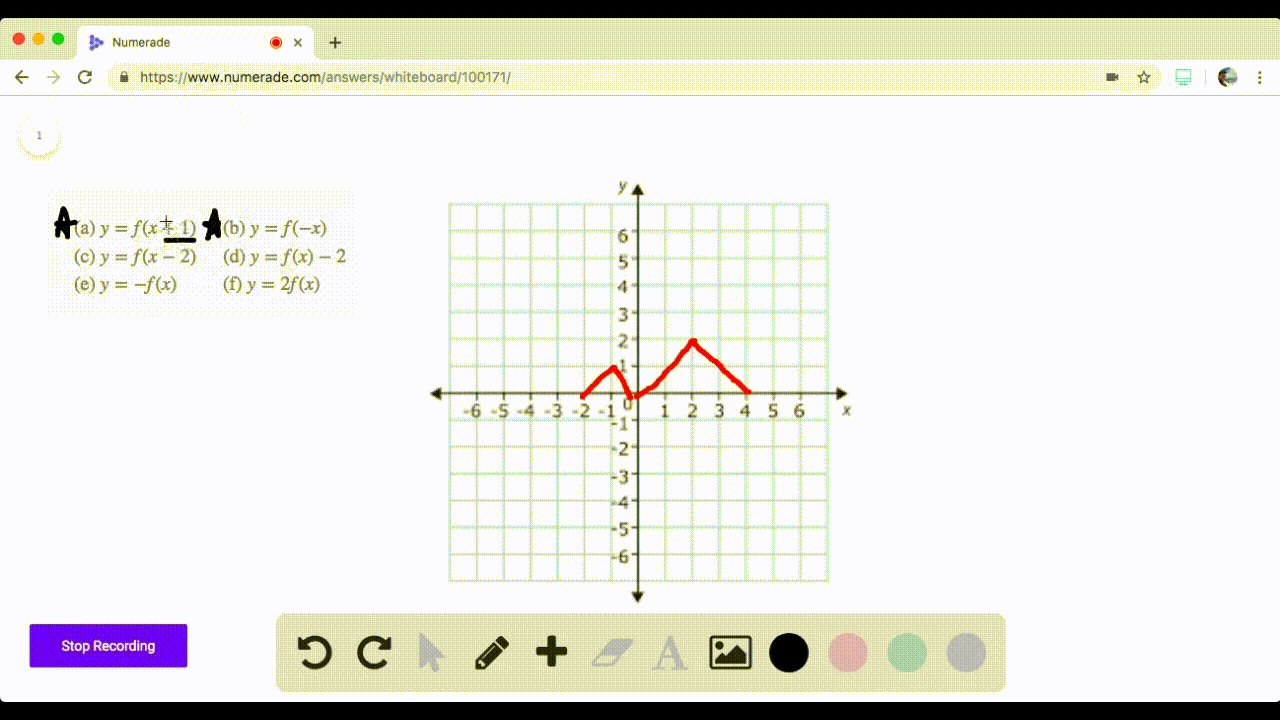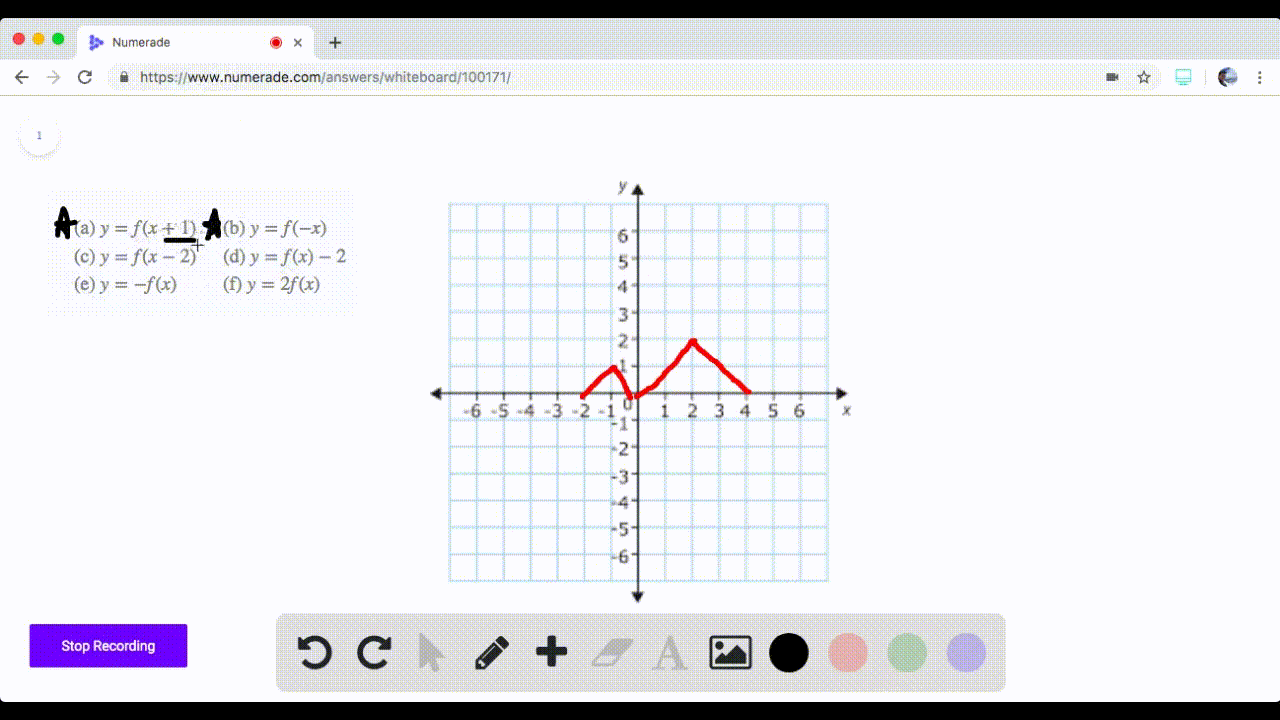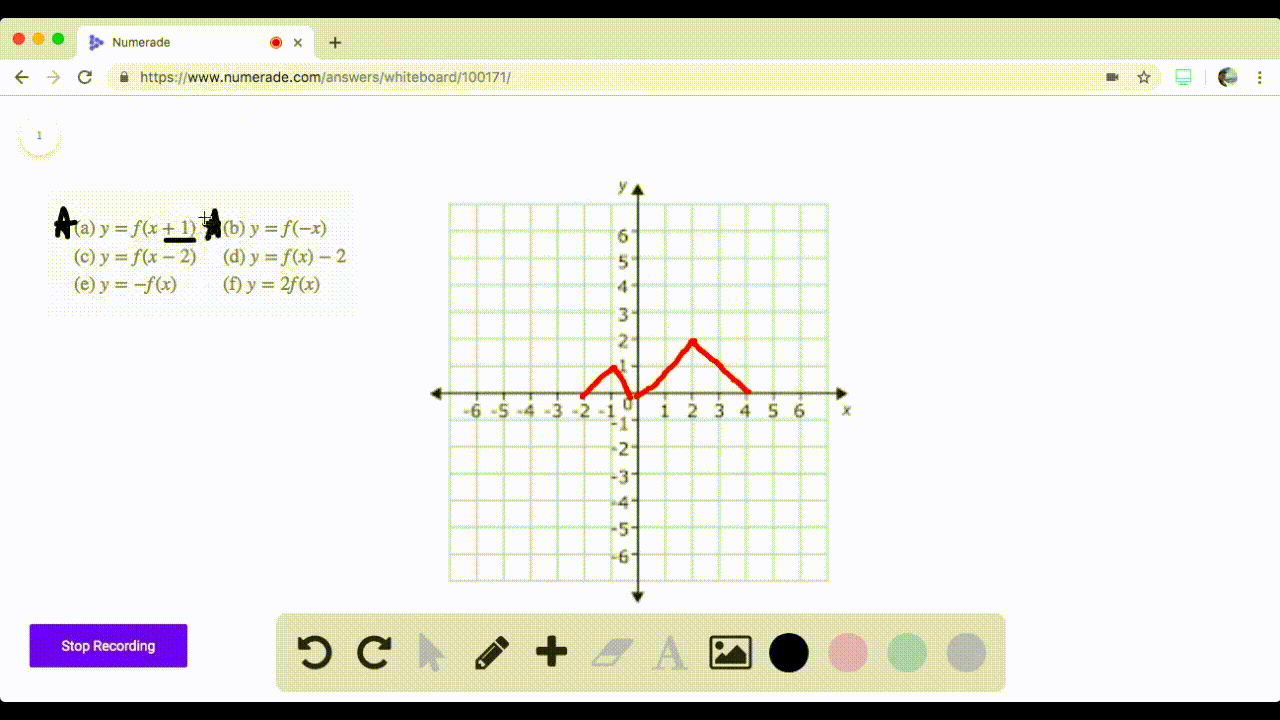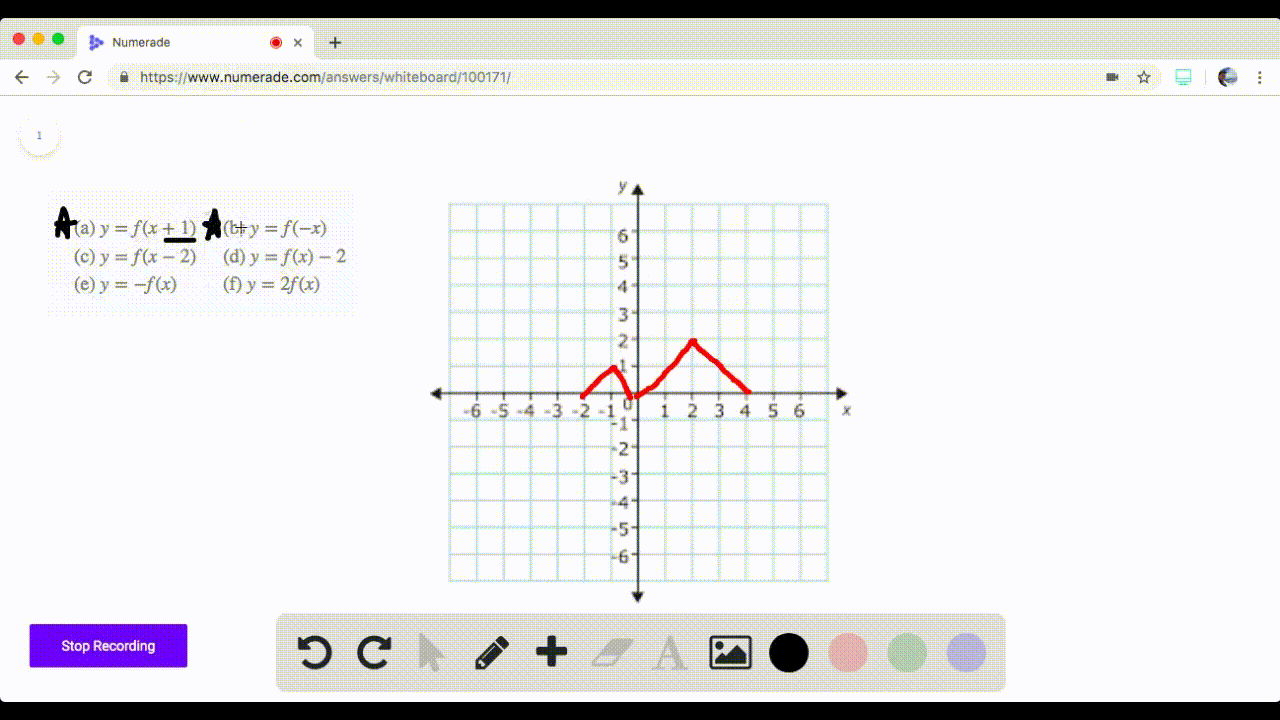



Solved 71 74 Graphing Transformations The Graph




Graphs Of Reciprocal Functions Video Lessons Examples And Solutions




Transformations Of Graphs Pdf Free Download



Ppt Transformations Of Graphs Powerpoint Presentation Free Download Id



Using Transformations To Graph Functions



Horizontal And Vertical Translations Of Exponential Functions College Algebra




Reflecting Functions Examples Video Khan Academy
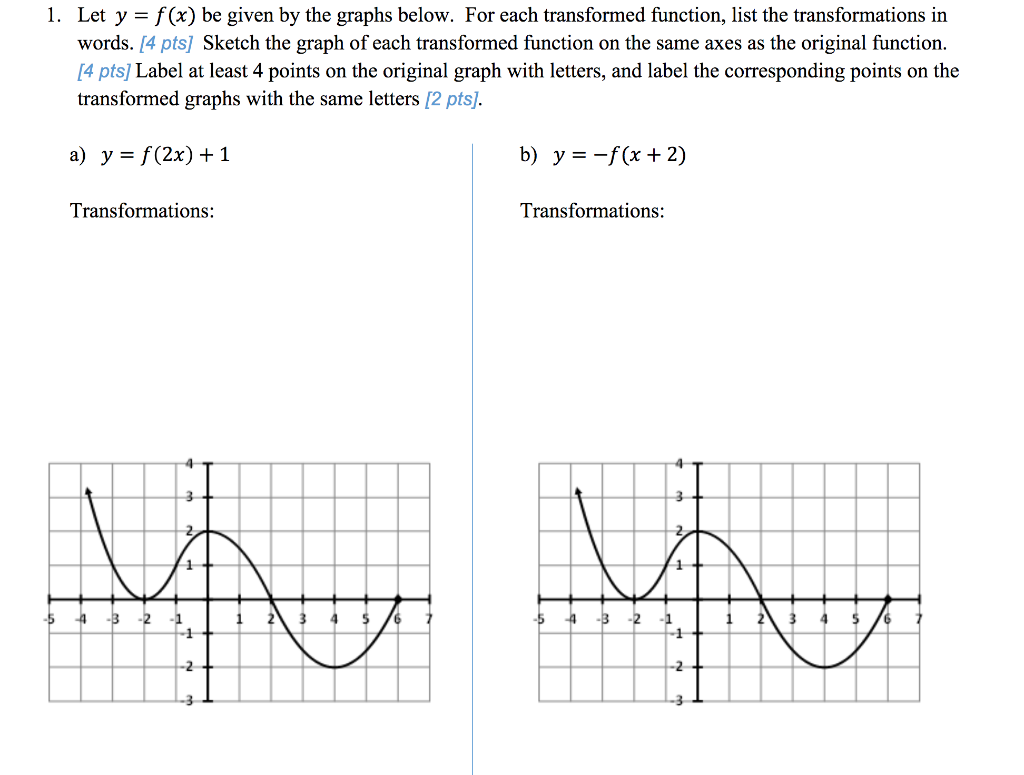



1 Let Y F X Be Given By The Graphs Below For Chegg Com



1 6 Vertical Transformations Mathematics Libretexts
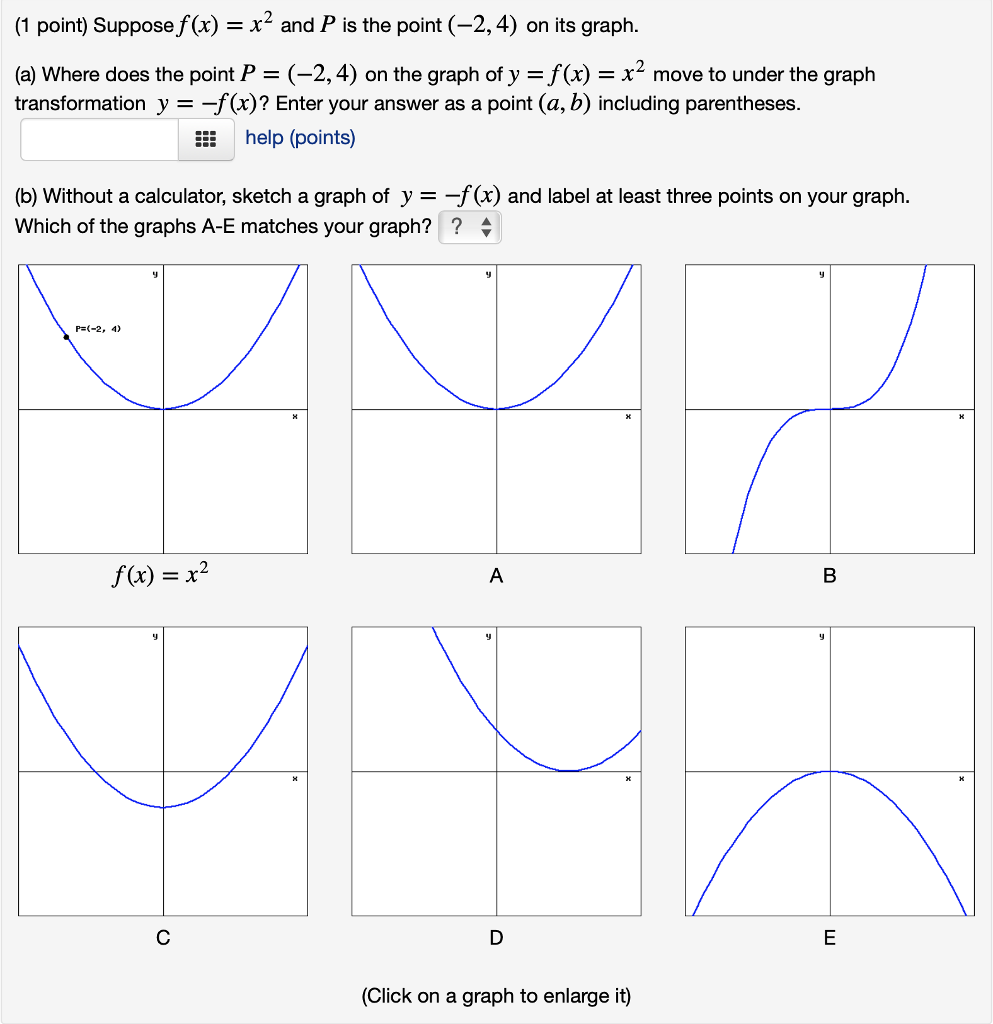



Solved 1 Point Suppose F X X2 And P Is The Point 2 4 Chegg Com




Finding The Equation Of A Transformation From The Graph Youtube



Example 1 Graphing A Function With Transformations Youtube




Consider The Graph Given Below Determine Which Sequences Of Transformations Could Be Applied To The Brainly Com
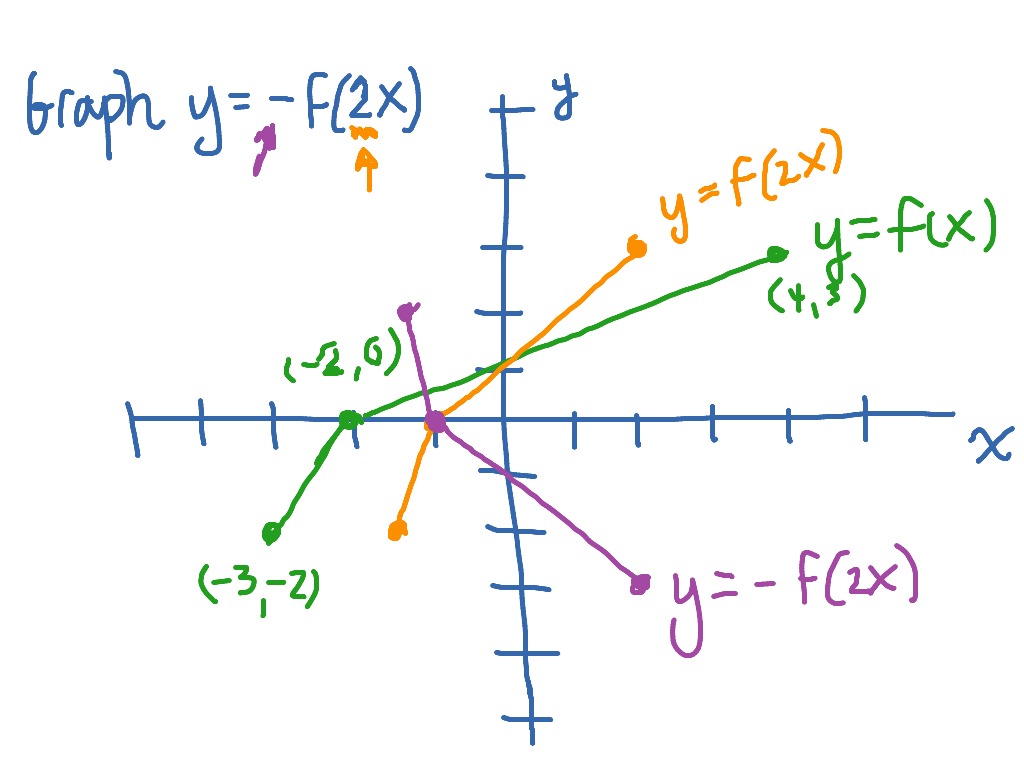



Graphing Y F 2x As A Transformation Of Y F X Math Showme



Transformations Math Help From Arithmetic Through Calculus And Beyond



Trasformations By Graph Paper Teacher Guide



Transformations Essential Algebra 2 Skills Sat Test Prep



Search Textbook Notes Pricing Log Insign Up Textbook Notes290 000 Ca170 000 Math 100 Chapter Function Transformations And Graphs Graphs On How To Draw Reflections Horizontal And Vertical Shifts 125 Views7 Pages Oc 14 Jun 17



Transformations Of Functions Part 1



Graphs Of Related Functions Ppt Download



The Graph Of The F X Is Show Below Graph Each Transformed Function And List In Words The Transformation Used Socratic



Graph Transformations Ppt Download




Transformation Of Graphs Maths Numeracy Educational School Posters



Answered 71 74 1 Graphing Transformations The Bartleby



Transformations Of Functions Definitions Facts And Solved Examples Cuemath



9 1 The Square Root Function Mathematics Libretexts



How To Reflect A Graph Through The X Axis Studypug




Transforming Functions Translations On Vimeo



What Happens When Y F 2x



Reflect Function About Y Axis F X Expii




Function Transformation Summary The Square Root Function Youtube



What Is A Function Transformation Expii



Transformations Math Help From Arithmetic Through Calculus And Beyond
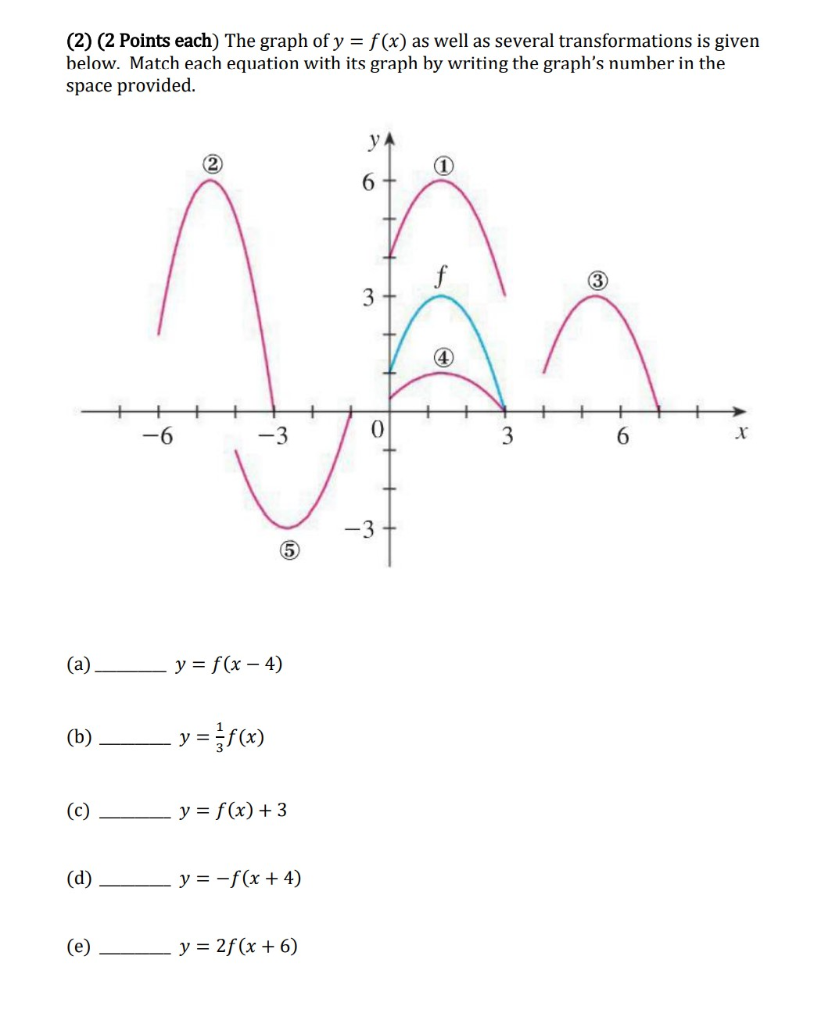



Solved 2 2 Points Each The Graph Of Y F X As Well Chegg Com
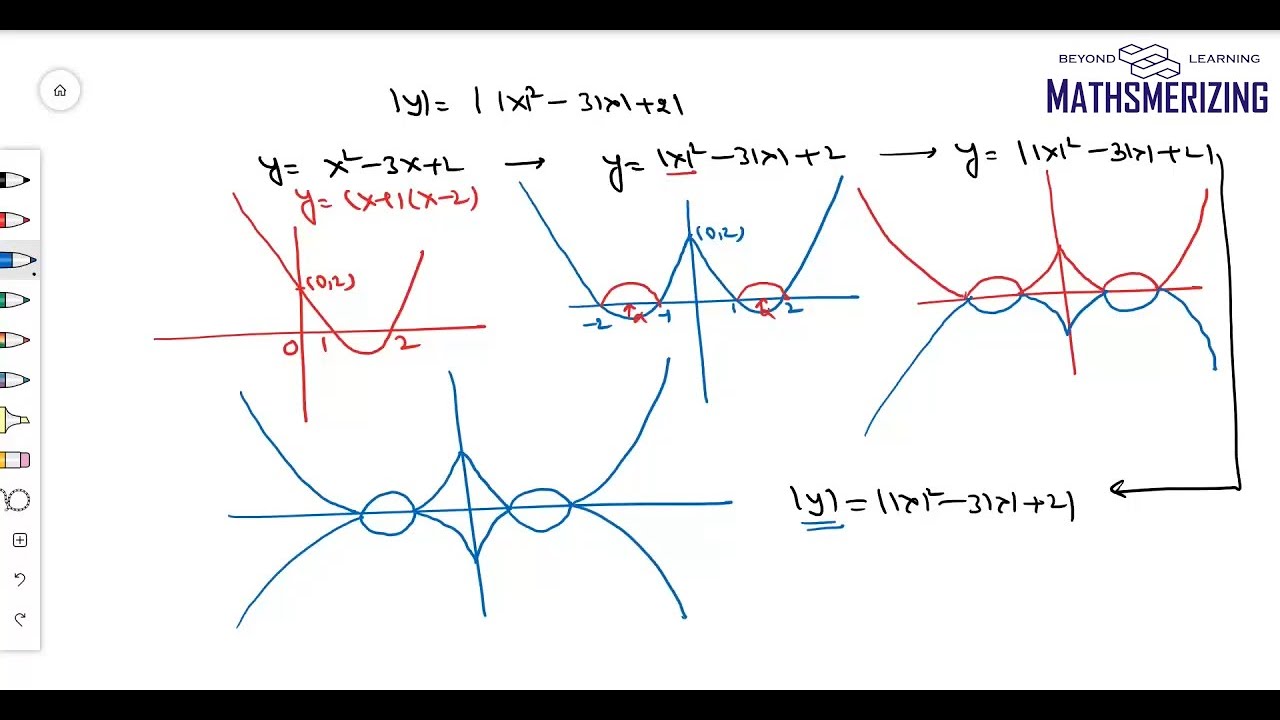



Transformation Of Graph L2 Modulus Function Graphs Of Y F X Y F X Y F X With Examples Youtube
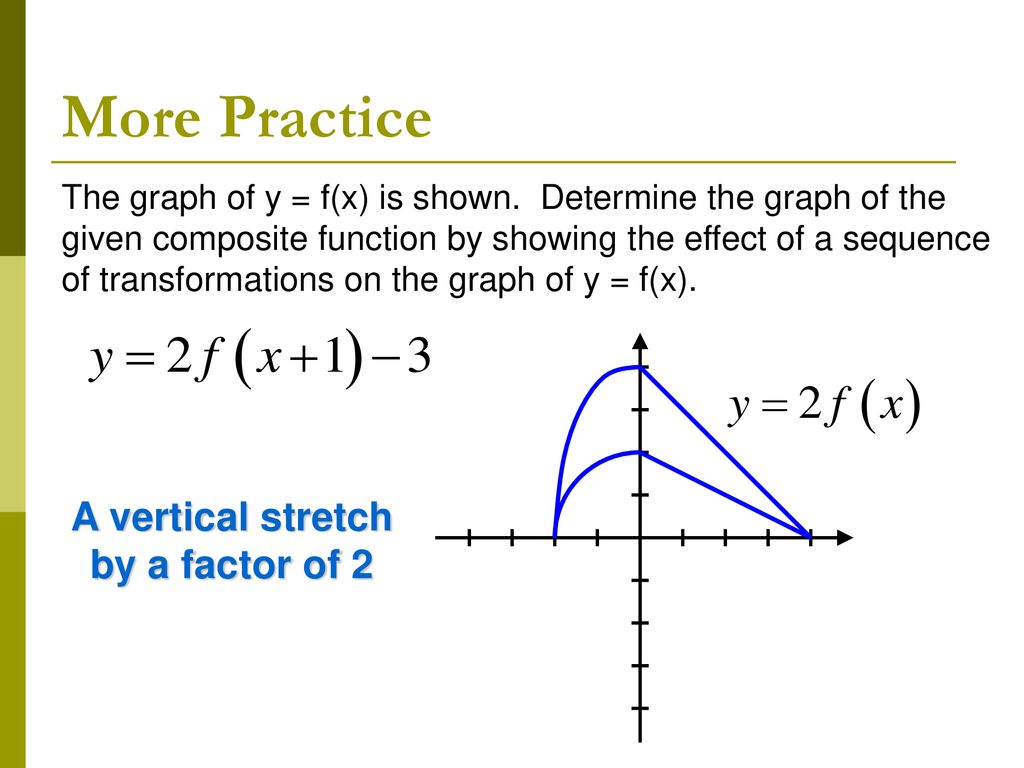



1 5b Combining Transformations Ppt Download
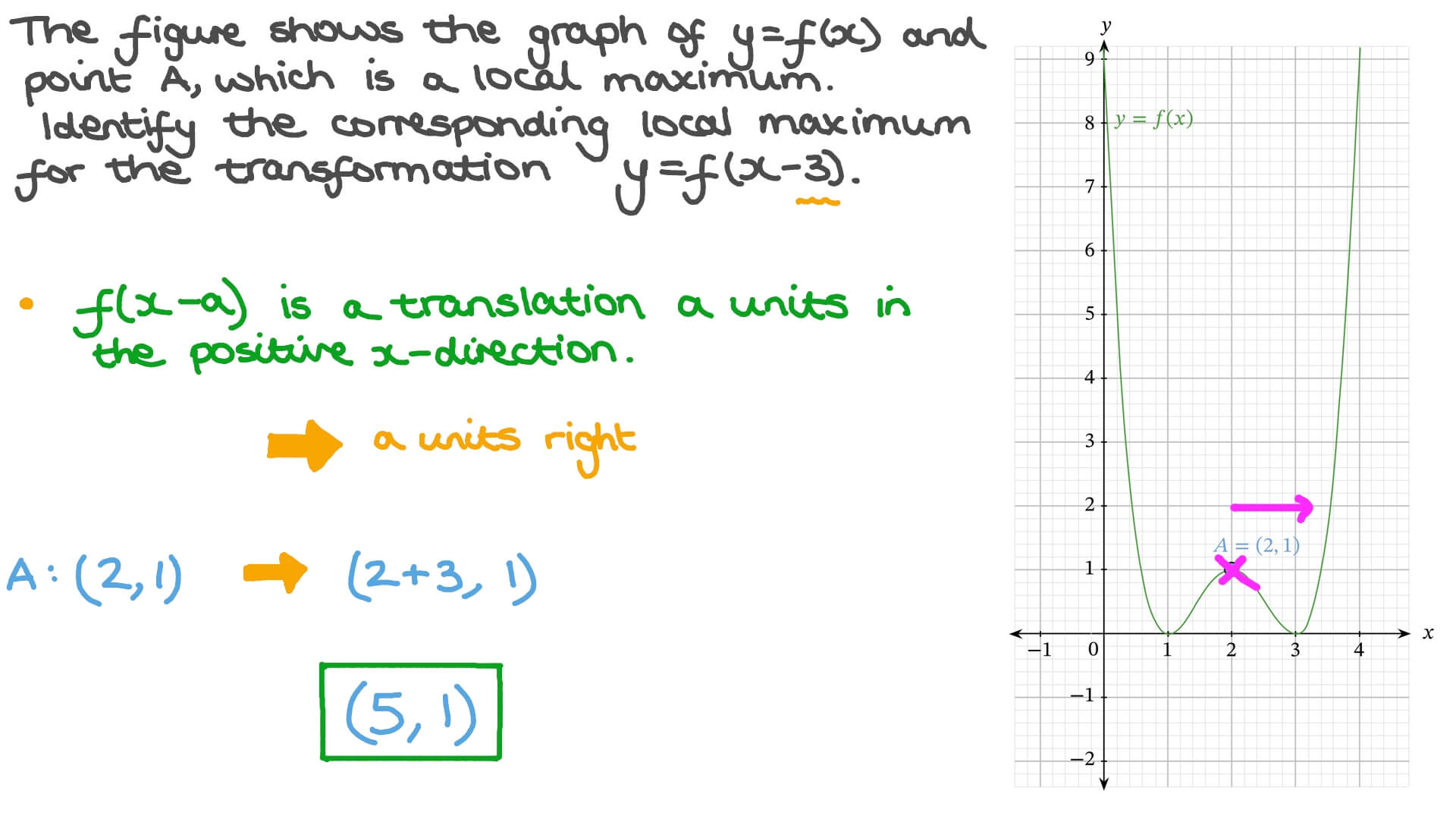



Question Video Identifying The Coordinates Of Points Following A Transformation Nagwa




Transformations Of Graphs Edexcel Igcse Maths Revision Notes
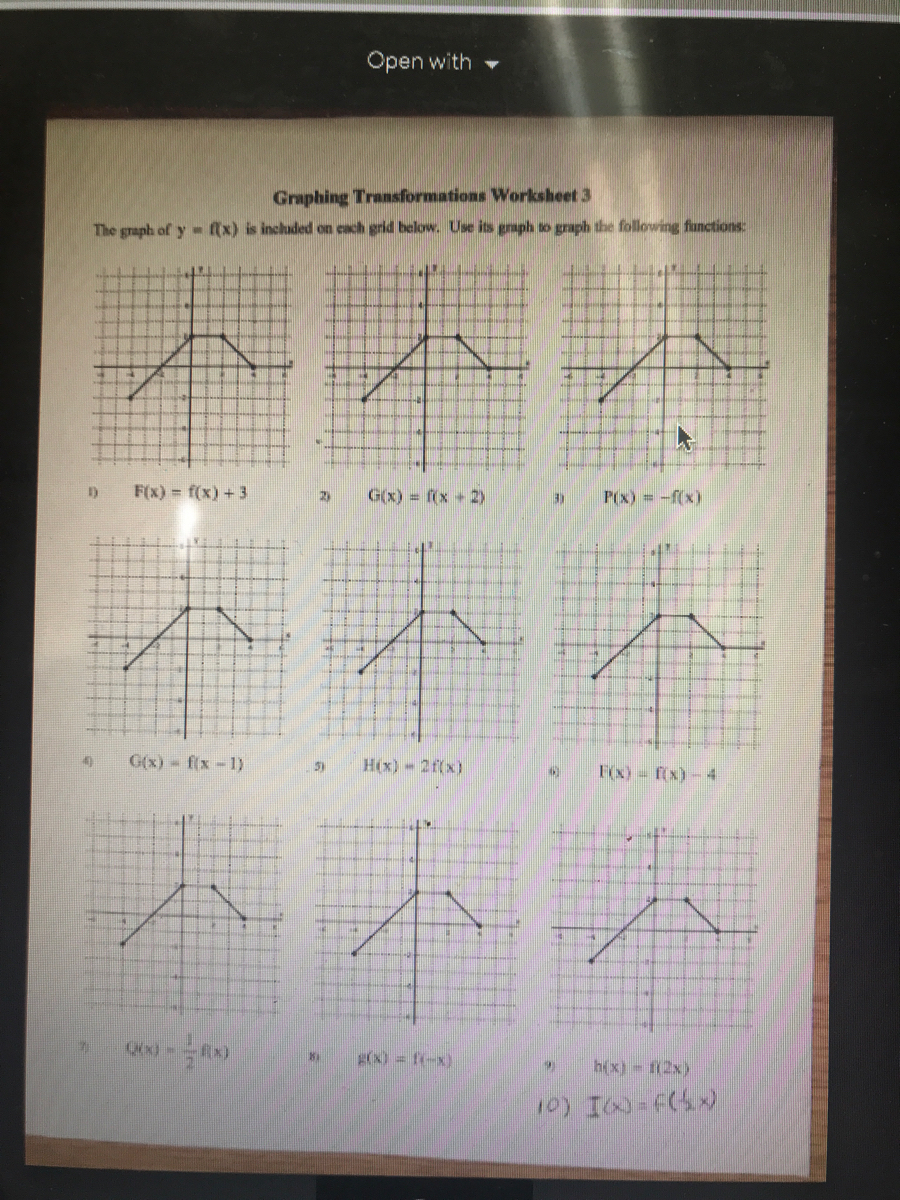



Answered Graphing Transformations Worksheet 3 Bartleby




Graph Transformations Rules Google Search Teaching Algebra High School Math Activities Learning Mathematics



Solved Transforming The Graph Of A Function By Reflecting Over An Axis A The Graph Of Y F X Is Shown Draw The Graph Of Y F X Ex X X



Solved O Graphs And Functions Transforming The Graph Of A Function By Reflecting Over An Axis A Thi V Hofy F X Is Shown Draw The Graph Of Y Course Hero
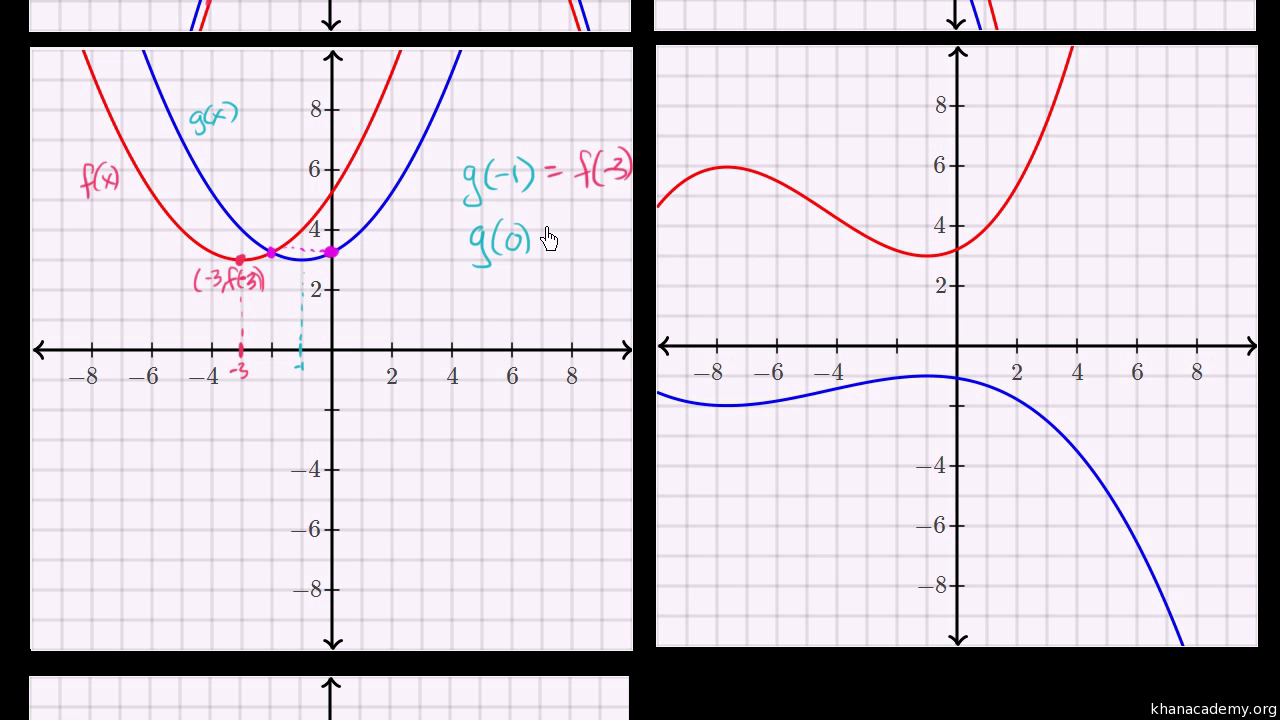



Identifying Function Transformations Video Khan Academy




Pin On Math Teachers Resources Blog
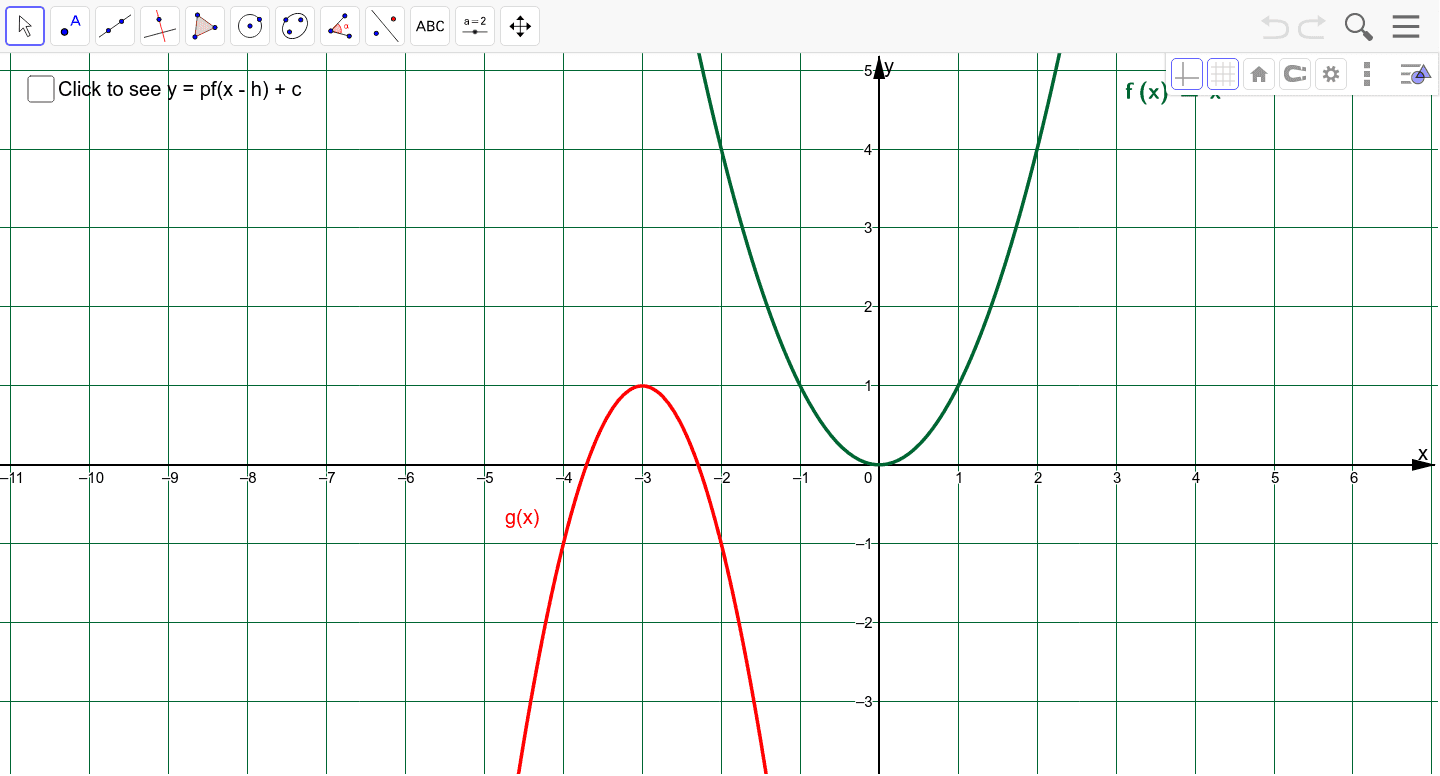



Transformation Of The Graph Of Y F X Geogebra




The Graph Of Y H X Is Shown Below The Function F X Is Defined By F X 1 2h X 3 A What Three Brainly Com




Ppt Graph Transformations Powerpoint Presentation Free Download Id




Lesson Video For Graph Square Root Functions Using Transformations Learnzillion



0 件のコメント:
コメントを投稿